Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

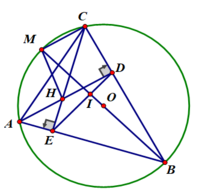
a) Xét tứ giác AEDC có:
∠(AEC) = ∠(ADC) = 90 0
Mà 2 góc này cùng nhìn cạnh AC
⇒ Tứ giác AEDC là tứ giác nội tiếp

a) Xét tứ giác AEDC có
\(\widehat{AEC}=\widehat{ADC}\left(=90^0\right)\)
\(\widehat{AEC}\) và \(\widehat{ADC}\) là hai góc cùng nhìn cạnh AC
Do đó: AEDC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

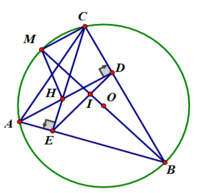
b) Xét ΔABD và Δ CEB có:
∠(ABC) chung
∠(ADB) = ∠(CEB) = 90 0
⇒ ΔABD ∼ Δ CBE (g.g)
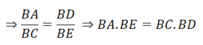

a) Xét tứ giác BNHM có
\(\widehat{BNH}\) và \(\widehat{BMH}\) là hai góc đối
\(\widehat{BNH}+\widehat{BMH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BNHM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

1.
Chứng minh được \widehat{CEB} = \widehat{BDC} = 90^{\circ}CEB=BDC=90∘.
Suy ra 44 điểm B,E, D, CB,E,D,C cùng thuộc đường tròn đường kính CBCB nên tứ giác BCDEBCDE nội tiếp.
Có tứ giác BCDEBCDE nội tiếp nên \widehat{DCE} = \widehat{DBE}DCE=DBE (22 góc nội tiếp cùng chắn cung DEDE) hay \widehat{ACQ} = \widehat{ABP}ACQ=ABP.
Trong đường tròn tâm (O)(O), ta có \widehat{ACQ}ACQ là góc nội tiếp chắn cung AQAQ và \widehat{ABP}ABP nội tiếp chắn cung APAP
\Rightarrow \overset{\frown}{AQ}=\overset{\frown}{AP}⇒AQ⌢=AP⌢.
2.
(O)(O) có \overset{\frown}{AQ}=\overset{\frown}{AP}



c) Do tứ giác AEDC là tứ giác nội tiếp nên ∠(CAB) = ∠(IDB) (cùng bù ∠(CDE) )
Mặt khác ∠(CAB) = ∠(CMB) (2 góc nội tiếp cùng chắn cung BC)
⇒ ∠(CMB) = ∠(IDB)
⇒ Tứ giác CMID là tứ giác nội tiếp ( Góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó)