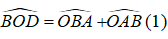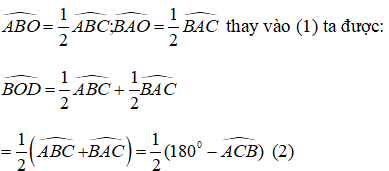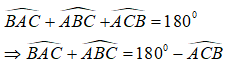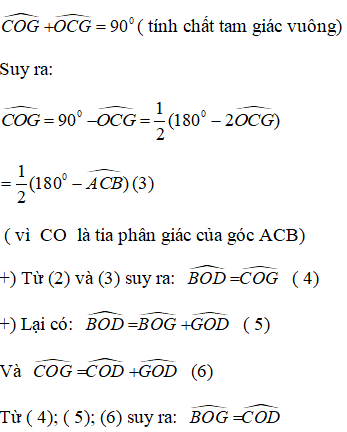Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A C B D M H x E F O
Ta giả sử \(\widehat{A}< 45^o\)
Gọi Hx là tia đối của tia HA.
trên Hx lấy HE = HA thì \(\widehat{CEA}=\widehat{CAE}\le45^o\). Do đó : \(\widehat{ACE}\ge90^o\)
Mà \(\widehat{ACB}>\widehat{ACE}\) vô lí ( trái với giả thiết cho \(\widehat{ACB}< 90^o\))
Gọi O là giao điểm của AD,BM,CH. Gọi F là giao điểm của EO và AC.
\(\Delta EAC\)có EA > EC ( vì EA đối diện với góc lớn hơn ) mà EF là phân giác của \(\widehat{AEC}\) , dễ chứng minh ) nên AF > FC
\(\Rightarrow AF>\frac{AC}{2}\). M là trung điểm của AC nên M nằm giữa A và F nên B thuộc tia Ex
Do đó : \(\widehat{ACB}>\widehat{ACE}\)mà \(\widehat{ACE}\ge90^o\)nên \(\widehat{ACB}>90^o\)( trái với giả thiết )
Vậy \(\widehat{A}>45^o\)
em gửi bài qua fb thầy HD cho, tìm fb của thầy bằng sđt: 0975705122, ở đây thầy không vẽ hình được
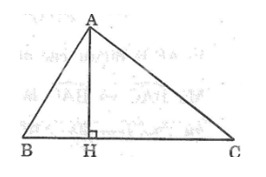
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .
Tham khảo:
(vì góc BOD là góc ngoài)
(Do BO,CO là các tia phân giác của tam giác ABC)
