Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABCABC không có góc tù (AB < AC)(AB<AC), nội tiếp đường tròn (O; R)(O;R), (BB, CC cố định, AA di động trên cung lớn BC). Các tiếp tuyến tại BB và CC cắt nhau tại MM. Từ MM kẻ đường thẳng song song với ABAB, đường thẳng này cắt (O)(O) tại DD và EE (DD thuộc cung nhỏ BCBC), cắt BCBC tại FF, cắt ACAC tại II. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra MBICMBIC là tứ giác nội tiếp.
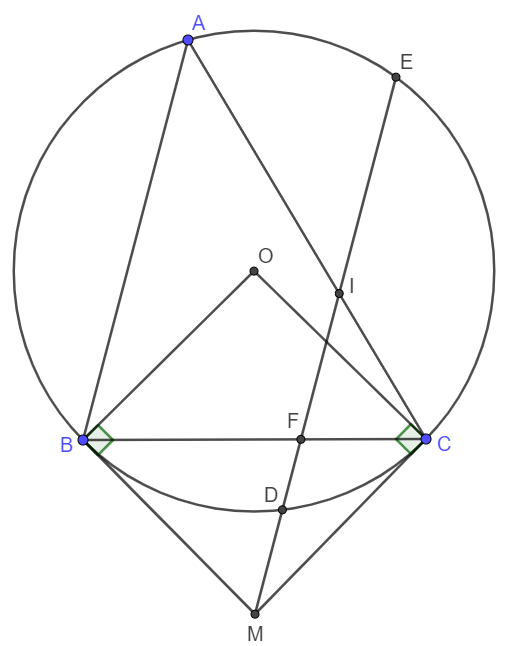
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep
a/ Ta có CF vuông góc AB tại F (gt)
Nên góc CFB = 90 độ
BE vuông góc AC tại E
Nên góc BEC = 90 độ
Tứ giác CEFB có hai đỉnh kề F và E cùng nhìn cạnh BC dưới một góc vuông . Do đó tứ giác CEFB nt
Ta có góc BFC = 90(cmt) độ nên tam giác BFC vuông tại F .
góc BEC = 90 độ (cmt)
Nên tam giác BEC vuông tại E
Tam giác vuông BFC và BEC đều có BC là cạnh huyền nên tâm của đường tròn ngoại tiếp tứ giác là trung điểm của cạnh BC .
a, Tứ giác BFEC có : \(\widehat{BFC}=\widehat{BEC}=90^0\), 2 góc này cùng nhìn cạnh BC
=> Tứ giác BFEC nội tiếp đường tròn tâm I , với I là trung điểm của BC và đường kính bằng BC
b, Xét tứ giác BFHD có : \(\widehat{BFH}+\widehat{BDH}=180^0\)
=> BFHD là tứ giác nội tiếp => \(\widehat{BHF}=\widehat{BDF}\)( tính chất 2 đỉnh kề nhau cùng nhìn xuống cạnh đối diện )
mà \(\widehat{BHF}+\widehat{BHC}=180^0\), \(\widehat{BDF}+\widehat{FDC}=180^0\)
=> \(\widehat{FDC}=\widehat{BHC}\)
Xét \(\Delta BHC\)và \(\Delta FDC\)có :
\(\widehat{C}\)chung
\(\widehat{FDC}=\widehat{BHC}\)
=> \(\widehat{CFD}=\widehat{HBC}\)
Lại có : Tứ giác BFEC nội tiếp đường tròn => \(\widehat{EBC}=\widehat{EFC\:}\)( tính chất 2 đỉnh kề nhau cùng nhìn xuống cạnh đối diện )
= > \(\widehat{CFD}=\widehat{EBC}\)( hay \(\widehat{HBC}\)) \(=\widehat{EFC\:}\)= > FC là tia phân giác của góc EFD
+, Xét \(\Delta ABE\)và \(\Delta ACF\)có :
\(\widehat{A}\)chung
\(\widehat{AEB}=\widehat{AFC}=90^0\)
= > 2 tam giác này đồng dạng = > \(\frac{AE}{AF}=\frac{AB}{AC}\)\(\Rightarrow AE.AC=AF.AB\)
1, Xét tứ giác BFEC có
^BFC = ^BEC = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tứ giác BFEC là tứ giác nt 1 đường tròn
tâm đường tròn ngoại tiếp tứ giác BFEC là trung điểm BC hay I là trung điểm cạnh BC
2, Xét tứ giác AEFH có ^AFH + ^AEH = 1800
mà 2 góc này đối
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
=> ^HFE = ^HAE ( góc nt chắn cung HE )
Xét tứ giác AFDC có
^AFC = ^ADC = 900
mà 2 góc kề, cùng nhìn cạnh CA
Vậy tứ giác AFDC là tứ giác nt 1 đường tròn
=> ^CAD = ^CFD ( góc nt chắn cung DC )
=> ^EFC = ^CED => FC là phân giác ^DFE
Xét tam giác AFE và tam giác ACB có
^A _ chung ; ^AFE = ^ACB ( góc ngoài đỉnh F của tứ giác BFEC )
Vậy tam giác AFE ~ tam giác ACB (g.g)
\(\frac{AF}{AC}=\frac{AE}{AB}\Rightarrow AF.AB=AE.AC\)