Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).

Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
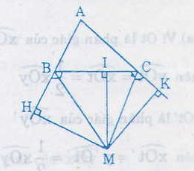
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc ˆBACBAC^
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)

Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của gócA

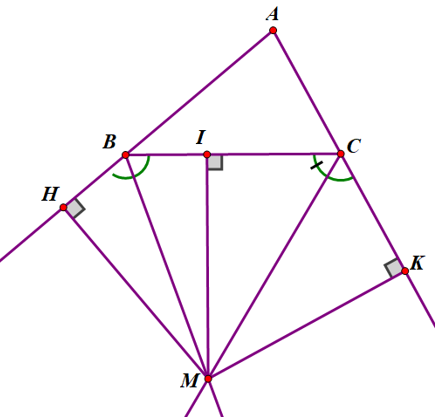
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
=>MH = MK (cùng= MI)
⇒ M thuộc phân giác của góc BAC

O A C B D E
a)Có: OC=OA+AC
OD=OB+BD
Mà : OA=OA(gt); AC=BD(gt)
=> OC=OD
Xét ΔOBC và ΔOAD có:
OC=OD(cmt)
\(\widehat{O}\) : góc chung
OB=OA(gt)
=> ΔOBC=ΔOAD(c.g.c)
=> BC=AD
b)Vì: ΔOBC =ΔOAD(cmt)
=> \(\widehat{OCB}=\widehat{ODA};\widehat{OBC}=\widehat{OAD}\) ( cặp góc tượng ứng)
Có: \(\widehat{OAD}+\widehat{DAC}=180^o\)
\(\widehat{OBC}+\widehat{CBD}=180^o\)
Mà: \(\widehat{OBC}=\widehat{OAD}\left(cmt\right)\)
=> \(\widehat{DAC}=\widehat{CBD}\)
Xét ΔEAC và ΔEBD có
\(\widehat{ECA}=\widehat{EDB}\left(cmt\right)\)
AC=BD(gt)
\(\widehat{EAC}=\widehat{EBD}\left(cmt\right)\)
=> ΔEAC=ΔEBD(g.c.g)
c) Vì: ΔEAC=ΔEBD(cmt)
=> EC=ED
Xét ΔOEC và ΔOED có:
OC=OD(cmt)
\(\widehat{OCE}=\widehat{ODE}\left(cmt\right)\)
EC=ED(cmt)
=> ΔOEC=ΔOED(c.g.c)
=> \(\widehat{EOC}=\widehat{EOD}\)
=> OE là tia pg của \(\widehat{xOy}\)
Xét ΔCOE và ΔDOE có:
OC=OD(cmt)
\(\widehat{COE}=\widehat{DOE}\left(cmt\right)\)
OE: cạnh chung
=> ΔCOE=ΔDOE(c.g.c)
=> \(\widehat{OEC}=\widehat{OED}=90^o\)

A B C O K
a) Ta có: + \(\widehat{BOC}\)là góc ngoài của tam giác OBK
=> \(\widehat{BOC}=\widehat{OBK}+\widehat{OKB}\) (1)
+ \(\widehat{OKB}\)là góc ngoài của tam giác AKC
=>\(\widehat{OKB}=\widehat{A}+\widehat{ACK}\)(2)
Từ (1)(2) =>\(\widehat{BOC}=\widehat{OBK}+\widehat{A}+\widehat{ACK}\)
hay\(\widehat{BOC}=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)
b) Ta có:\(\widehat{ABO}+\widehat{ACO}=90^o-\frac{\widehat{A}}{2}\)
=>\(2\widehat{ABO}+2\widehat{ACO}=180^o-\widehat{A}\)(3)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)( Tổng 3 góc trong 1 tam giác)
=>\(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{A}\)(4)
Từ (3)(4) => \(2\widehat{ABO}+2\widehat{ACO}=\widehat{ABC}+\widehat{ACB}\)(*)
Ta có: BO là tia phân giác của góc ACB
=>\(2\widehat{ABO}=\widehat{ABC}\)(**)
Từ (*)(**) => \(2\widehat{ABO}+2\widehat{ACO}=2\widehat{ABO}+\widehat{ACB}\)
=>\(2\widehat{ACO}=\widehat{ACB}\)
=> CO là tia phân giác của góc ACB

Hình tự vẽ nha
Giải : Kẻ DI vuông góc với AB, DK vuông góc với AC. Xét ΔADC và ΔADB : các đường cao DI = DK, các đáy AC = 2 AB nên SADC = 2 SADB. Vẫn xét hai tam giác trên có chung đường cao kẻ từ A đến BC, do SADC = 2 SADB nên DC = 2 DB. Giải tương tự như trên, ta chứng minh được bài toán tổng quát : Nếu AD là phân giác của ΔABC thì DB/DC = AB/AC. Bài toán 2 : Cho hình thang ABCD (AB // CD), các đường chéo cắt nhau tại O. Qua O, kẻ đường thẳng song song với hai đáy, cắt các cạnh bên AC và BC theo thứ tự tại E và F. Chứng minh rằng OE = OF
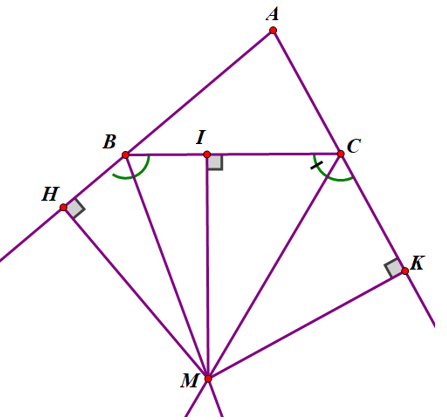


Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
Theo định lí thuận về tính chất các điểm thuộc tia phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí đảo về tính chất các điểm thuộc tia phân giác: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).