Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Xét tam giác ABM và tam giác ACM có :
góc B = góc C (gt )
AB=AC ( gt )
góc A1 = góc A2 (gt )
suy ra : tam giác ABM = tam giác ACM ( g - c -g )
b )
ta có : tam giác ABM = tam giác ACM suy ra : BM = CM = BC : 2 = 3 (cm )
Theo định lí pitago trong tam giác vuông ABM có :
AB2 = AM2 + BM2
SUY RA : AM2 = AB2 - BM2
AM2 = 52 - 32
AM = căn bậc 2 của 16 = 4 (cm )
c )
Do D nằm giữa 2 điểm M và C nên ta có :
MD + DC = MC
suy ra : MC > MD
Đúng thì nha bạn

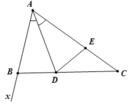
b. Giả sử góc ngoài tại đỉnh B của tam giác ABC là ∠(xBC). Ta có:
∠(xBC) + ∠(ABD) = 180o ⇒ ∠(xBC) = 180o - ∠(ABD) (0.5 điểm)
∠(DEC) + ∠(AED) = 180o ⇒ ∠(DEC) = 180o - ∠(AED) (0.5 điểm)
Mà ∠(ABD) = ∠(AED) ( hai góc tương ứng vì ΔABD = ΔAED)(0.5 điểm)
Từ đó suy ra ∠(xBC) = ∠(DEC) (0.5 điểm)

a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: góc FBC+góc C=90 độ
góc MAC+góc C=90 độ
=>góc FBC=góc MAC