Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)( Hai góc kề bù )
\(\widehat{ACB}+\widehat{ACE}=180^0\)( Hai góc kề bù )
Mà \(\widehat{ABC}=\widehat{ACB}\)( Do tam giác ABC cân ở A )
=> \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ABD và tam giác ACE có:
AB = AC ( Do tam giác ABC cân ở A )
\(\widehat{ABD}=\widehat{ACE}\)( cmt )
BD = CE ( gt )
=> Tam giác ABD = tam giác ACE ( c.g.c )
=> AD = AE ( hai cạnh tương ứng )
b) Ta có:
BD + BM = DM
CE + CM = EM
Mà DB = CE ( gt ), BM = CM ( Do M là trung điểm )
=> DM = EM
Xét tam giác AMD và tam giác AME có:
AD = AE ( cmt )
AM chung
DM = EM ( cmt )
=> Tam giác AMD = tam giác AME ( c.c.c )
=> \(\widehat{DAM}=\widehat{EAM}\)( Hai góc tương ứng )
b) Vì tam giác ABD = tam giác ACE ( cmt )
=> \(\widehat{ADB}=\widehat{ACE}\)( Hai góc tương ứng )
Xét tam giác BHD và tam giác CKE có:
\(\widehat{BHD}=\widehat{CKE}\left(=90^0\right)\)
Cạnh huyền: BD = CE ( gt )
Góc nhọn: \(\widehat{ADB}=\widehat{ACE}\)( cmt )
=> Tam giác BHD = tam giác CKE ( cạnh huyền - góc nhọn )
=> BH = CK ( hai cạnh tương ứng )
# Học tốt #

a) Tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ACB}\)
Hay \(\widehat{ABD}=\widehat{ACE}\)
Theo định lý Cos ta có
\(AD=\sqrt{DB^2+AB^2-2\cdot DB\cdot AB\cdot\cos DBA}\)
\(AE=\sqrt{AC^2+CE^2-2\cdot AC\cdot CE\cdot\cos ACE}\)
Vì AB = AC ( tam giác ABC cân tại A ) và DB =CE và góc DBA = góc ACE
Nên AD = AE hay tam giác ADE cân tại A
b)\(\widehat{ADB}=\widehat{AEC}\)(ADE cân)
Nên góc KCE = góc DBH
Vậy \(\widehat{HBA}=\widehat{KCA}\)( góc DBA = góc ACE)
Xét tam giác HBA và tam giác ACK vuông có :
+ góc HBA = góc KCA
+ AB = AC
\(\Rightarrow\Delta HBA=\Delta KCA\left(ch-gn\right)\)=> HB = KC (hai cạnh tương ứng)
c) Ta có \(180^0=\widehat{HBA}+\widehat{ABC}+\widehat{OBC}\)
\(180^0=\widehat{ACK}+\widehat{ACB+\widehat{OCB}}\)
\(\widehat{HBA}=\widehat{ACK}\)
\(\widehat{ABC}=\widehat{ACB}\)
Nên \(\widehat{OCB}=\widehat{OBC}\)hay tam giâc OBC cân tại O
d) Xét tam giác AMB và tam giác AMC
+ AM chung
+ BM = MC (gt)
+ AB = AC (gt)
Vậy hai tam giác trên bằng nhau theo trường hợp c-c-c
Và hai góc BAM = góc CAM
Hay AM là tia phân giác của góc BAC
Xét tam giác AOB và tam giác ACO
+ AB = AC (gt)
+ OB = OC (cmt )
+ góc ABO = góc ACO vì \(\widehat{ABM+\widehat{OBC}=\widehat{ACM}+\widehat{OCB}}\)
Vậy hai tam giác trên bằng nhau theo trường hợp c-g-c
Và góc BAO = góc CAO
Hay AO là phân giác của góc BAC
Một góc chỉ có duy nhất một tia phân giác nên AM và AO là một hay A,M,O thẳng hàng

XÉT TAM GIÁC ABD VÀ TAM GIÁC ACE CÓ
AB=AC(GT)
DB=CE (GT)
\(\widehat{ABD}+B1=180^O\)
\(\widehat{ACE}+\widehat{C_1}=180^0\)
=>\(\widehat{ABD}+\widehat{B_1}=\widehat{ACE}+\widehat{C_1}\)
MÀ GÓC B1 = GÓC C1
=>\(\widehat{ABD}=\widehat{ACE}\)
=>\(\Delta ADB=\Delta ACE\left(CGC\right)\)
=>AD=AE
=> \(\Delta ADE\) CÂN TẠI A
B,XÉT TAM GIÁC HBD VÀ TAM GIÁC CKE CÓ
DB=CE (GT)
\(\widehat{H}=\widehat{K}=90^0\)
\(\widehat{D}=\widehat{E}=90^0\) VÌ TAM GIÁC ADE CÂN TẠI A
=> TAM GIÁC DHB= TAM GIÁC CKE (GCG)
=>BH=CK(CẠNH TƯƠNG ỨNG)
C,XÉT TAM GIÁC ABM VÀ TAM GIÁC ACN CÓ
\(\widehat{M}=\widehat{N}=90^0\)
AB=AC (GT)
\(\widehat{NAC}=\widehat{MAB}\) VÌ (\(\widehat{A_1}+\widehat{A_2}=\widehat{A_2}+\widehat{A_3}\))
=>TAM GIÁC ABM = TAM GIÁC ACN (GCG)
=>BM=CN ( CẠNH TƯƠNG ỨNG)

A B C D K E H
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^o\) (kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^o\)(kề bù)
Mà \(\widehat{ABC}=\widehat{ACB}\) (do \(\Delta ABC\) cân tại A)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét hai tam giác ABD và ACE có:
\(\widehat{BAD}=\widehat{CAE}\) (gt)
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
Vậy: \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
Suy ra: BD = CE (hai cạnh tương ứng)
b) Xét hai tam giác BHD và CKE có:
BD = CE (cmt)
\(\widehat{ADB}=\widehat{AEC}\) (\(\Delta ABD=\Delta ACE\))
Vậy: \(\Delta BHD=\Delta CKE\left(ch-gn\right)\)
Suy ra: BH = CK (hai cạnh tương ứng).

A B C D E H K
a) Vì \(\Delta ABC\) cân tại A
=> \(\widehat{B}=\widehat{C}\)
mà \(\widehat{ABD}+\widehat{ABC}=180^0\) (kề bù)
và \(\widehat{ACB}+\widehat{ACE}=180^0\) (kề bù)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta ABC\) và \(\Delta ACE\) có:
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
DB = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
=> \(\widehat{D}=\widehat{E}\) ( hai góc tương ứng)
Xét \(\Delta DBH\) và \(\Delta ECK\) có:
\(\widehat{DHB}=\widehat{CKE}\) ( = 900)
DB = CE (gt)
\(\widehat{D}=\widehat{E}\)(cmt)
Do đó: \(\Delta DBH=\Delta ECK\) (ch -gn)
=> BH = CK (hai cạnh tương ứng)
b) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
CK = BH ( cmt )
\(\widehat{AHB}=\widehat{AKC}\left(=90^0\right)\)
AB = AC (gt)
Do đó: \(\Delta ABH=\Delta ACK\) ( cạnh huyền - cạnh góc vuông)
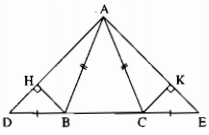
a) Vì ∆ABC cân tại A nên góc ABC =góc ACB (tính chất tam giác cân)
Ta có: góc ABC + góc ABD=180o (hai góc kề bù)
góc ACB + góc ACE=180o (hai góc kề bù)
Suy ra: góc ABD = góc ACE
Xét ∆ABD và ∆ACE, ta có:
AB = AC (gt)
góc ABD = góc ACE (chứng minh trên)
BD = CE (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
⇒ góc D = góc E (hai góc tương ứng)
Xét hai tam giác vuông BHD và CKE, ta có:
góc BHD =góc CKE=90o
BD = CE (gt)
góc D = gócE (chứng minh trên)
Suy ra: ∆BHD = ∆CKE (cạnh huyền, góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Xét tam giác vuông AHB và ACK, ta có:
góc AHB = gócAKC = 90o
AB = AC (gt)
BH = CK (chứng minh trên)
Suy ra: ∆ABH = ∆ACK (cạnh huyền, cạnh góc vuông)

Bài làm
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)
\(\widehat{ACB}+\widehat{ACE}=180^0\)
Mà \(\widehat{ABC}=\widehat{ACB}\)( Do tam giác ABC cân ở A )
=> \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ABD và tam giác ACE có:
AB = AC ( Do tam giác ABC cân ở A )
\(\widehat{ABD}=\widehat{ACE}\)( cmt )
DB = CE ( cmt )
=> Tam giác ABD = tam giác ACE ( c.g.c )
=> AD = AE ( hai cạnh tương ứng )
b) Mik chưa hiểu ý câu b cho lắm, vì đề bài chưa cho điểm N thì điểm N chui từ đâu ra?
c) Vì tam giác ABD = tam giác ACE ( cmt )
=> \(\widehat{ADB}=\widehat{AEC}\)
Xét tam giác HBD và tam giác KCE có:
\(\widehat{BHD}=\widehat{CKE}\left(=90^0\right)\)
Cạnh huyền: BD = CE ( gt )
Góc nhọn: \(\widehat{ADB}=\widehat{AEC}\) ( cmt )
=> Tam giác HBD = tam giác KCE ( cạnh huyền - góc nhọn )
=> BH = CK ( đpcm )
# Học tốt #