Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

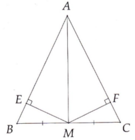
Xét `△BEM` và `△ CFM`:
\(\widehat{MEB}=\widehat{CFM}\)
`BM = MC`
\(\widehat{EBM}=\widehat{FCM}\)
`=>△BEM = △ CFM`
`=> BE = FC`
Ta có:
` AB = AE + EB`
` AC = AF + FC`
Mà `AB = AC` (vì △ABC cân tại A)
`EB = FC (cmt)`
`=> AE = AF`
`=>` △AEF` cân tại A
Xét `△AEM` và `△AFM` có:
AE = AF
\(\widehat{AEM}=\widehat{AFM}\)
AM cạnh chung
`=> △AEM =△AFM`
`=>` \(\widehat{EAM}=\widehat{FAM}\)
`=> AM là đường phân giác
Xét △AEF cân tại A có:
AM là đường phân giác
`=>` AM là trung trực của BC
b) Ta có: △AEM =△AFM
=> ME = MF
Xét △AEF cân tại A có:
AM là đường phân giác
=> AM là đường trung trực của EF

a) sửa đề => đường trung trực
ta có tg ABC cân tại A
M là trung điểm của BC
=> AM là đường trung trực của BC
=> AM là đường pg của tg ABC (t/c tg cân )
=> gBAM = gCAM hay gEAM = gFAM
xét tg AME và tg AMF có
gEAM = gFAM (cmt)
AM chung
gAEM = gAFM (=90o)
=> tg AME = tgAMF (cạnh huyền góc nhọn )
=> ME = MF (2 cạnh t/ư )

A B C E F M D
Vì tam giác ABC cân tại A
suy ra AB = AC, góc B = góc C
Xét tam giác vuông BME và tam giác vuông CMF
có Bm=CM (GT)
góc EBM = góc FCM ( CMT)
suy ta tam giác EBM = tam giác FCM ( cạnh huyền-góc nhọn)
suy ra EM=MF (hai cạnh tương ứng)
BE=CF (hai cạnh tương ứng)
mà BE+EA=AB, AF+FC=AC, lại có AB=AC
suy ra AE=AF
Xét tam giác AEM và tam giác AFM
có AE=AF (CMT)
AM chung
EM=FM ( CMT)
suy ra tam giác AEM = tam giác AFM (c.c.c) (*)
suy ra AE=AF suy ra A thuộc đường trung trực của EF (1)
mà MF=MF (CMT) suy ra M thuộc đường TT của EF (2)
Từ (1) và (2) suy ra AM là đường T.T của EF
b) Xét tam giác ABD và tam giác ACD
có AD chung
AB=AC (CMT)
góc ABD=góc ACD = 900
suy ra tam giác ABD và tam giác ACD (cạnh huyền-cạnh góc vuông)
suy ra góc BAD = góc CAD
suy ra AD là tia phân giác của góc BAC (3)
Từ (*) suy ra góc EAM = góc CAM
suy ra AM là tia phân giác của góc BAC (4)
Từ (3) và (4) suy ra AM trùng AD
suy ra A, M, D thẳng hàng

A B C M E F D 1 2 K
Xét tam giác ABM và tam giác ACM
có : + AB = AC (gt)
+ BM = CM (gt)
+) AM chung
=> tam giác ABM = tam giác ACM (c.c.c)
=> góc A1 = góc A2
Xét tam giác AEM và tam giác AFM có :
+) góc AME = góc AMF (Vì góc MEA = MFA (= 90o) ; góc A1 = góc A2 => góc MEA - góc A1 = góc MFA - góc A2 => <AME = <AMF)
+ góc A1 = góc A2
+) AM chung
=> Tam giác AEM = Tam giác AFM (g.c.g)
=> ME = MF (cạnh tương ứng)
=> AE = AF
b) Gọi K là giao điểm của AM và EF
Xét tam giác AEK và tam giác AFK có
+) góc A1 = góc A2
+) AF = AE (cmt)
+) AK chung
=> tam giác AEK = tam giác AFK (c.g.c)
=> EK = FK (cạnh tương ứng)
=> góc AKE = góc AKF (góc tương ứng)
Lại có góc AKE + góc AKF = 180 o
=> góc AKE = góc AKF = 90o
mà EK = FK
=> AK là trung trực của EF
mà K \(\in\)AM
=> AM là trung trực của EF
c) Vì tam giác ABM = tam giác ACM (cmt)
=> góc AMB = góc AMC
Mà góc AMB + góc AMC = 180 o
=> góc AMB = góc AMC = 90o
lạ có MC = MB = 1/2BC
=> AM là trung trực của BC (1)
Vì góc AMB = góc AMC = 90o
mà góc AMB + góc BMD = góc AMC + góc CMD (=180o)
=> góc BMD = góc CMD = 90o
lại có BM = CM = 1/2BC
=> MD là trung trực của BC (2)
Từ (1) (2) => A;M;D thẳng hàng