Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AH=8cm
b: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
c: Xét ΔADH và ΔAEH có
AD=AE
\(\widehat{DAH}=\widehat{EAH}\)
AH chung
Do đó ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
d: Ta có:AD=AE
HD=HE
Do đó:AH là đường trung trực của DE

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

1: AH=8cm
2: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
4: Xét ΔABC có AD/AB=AE/AC
nên DE//BC

1, Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-BH^2}=8cm\)
2, Xét tam giác ABH và tam giác ACH có
AB = AC ; AH _ chung
Vậy tam giác ABH = tam giác ACH (ch-cgv)
3, Vì tam giác ABC cân tại A có AH là đường cao
đồng thời là phân giác
Lại có DB = CE ; AB = AC
=> AD = AE
Xét tam giác ADH và tam giác AEH có
AD = AE ( cmt ) ; AH _ chung ; ^DAH = ^EAH
Vậy tam giác ADH = tam giác AEH (c.g.c)
=> DH = HE ( 2 cạnh tương ứng )
Vậy tam giác HDE cân tại H
4, Ta có AD/AB = AE/AC => DE//BC
 tham khao
tham khao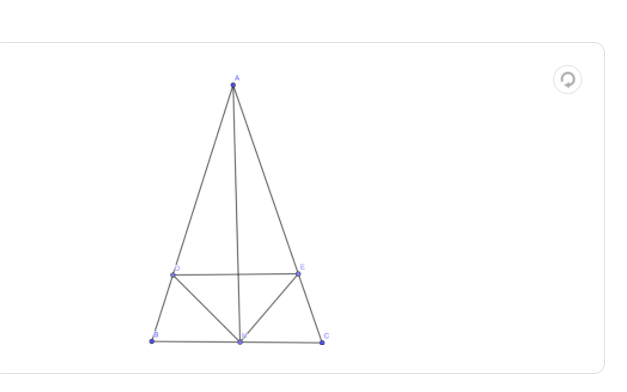
a, Xét tam giác HBA vuông tại H có:
\(AB^2=AH^2+BH^2\) (định lí py ta go)
hay \(100=AH^2+36\)
=> \(AH^2=64\)
=> AH=8(cm)
b, Xét tam giác ABH và tam giác ACH có:
góc AHB=góc AHC =90 độ
AB=AC (tam giác ABC cân tại A)
AH chung
=> tam giác ABH = tam giác ACH
c,
Xét tam giác DBH và tam giác ECH có:
BD=CE (gt)
góc DBH= góc ECH (tam giác ABC Cân tại A)
BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)
=> tam giác DBH=tam giác ECH
=> DH=EH( 2 cạnh tương ứng)
=> tam giác HDE cân tại H
A B C H 6 10 D 6 10 E