Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
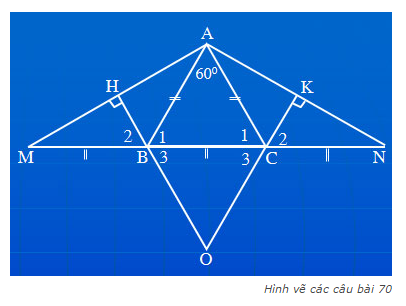
a.Vì tam giác ABC cân tại A nên AB= AC và góc ABC = góc ACB
<=> góc ABM = góc ACN (vì các góc kề bù với nhau)
Xét tam giác ABM và tam giác ACN
Có: AB = AC (CMT)
góc ABM = góc ACN (CMT)
BM = CN (gt)
<=> tam giác ABM = tam giác ACN (c.g.c)
<=> AM = AN ( 2 góc tương ứng)
<=> tam giác AMN cân tại A
b. Vì tam giác ABM = tam giác ACN (CMT)
<=> góc MAB = góc CAN ( 2 góc tương ứng)
Xét tam giác vuông AHB và tam giác vuông AKC
Có: AB= AC (CMT)
góc AHB= góc AKC= 90 độ
góc MAB = góc CAN (CMT)
<=> tam giác AHB = tam giác AKC ( cạnh huyền- góc nhọn)

a) Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACN}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN(gt)
\(\widehat{HMB}=\widehat{KNC}\)(hai góc ở đáy trong ΔAMN cân tại A)
Do đó: ΔHBM=ΔKCN(cạnh huyền-góc nhọn)
Suy ra: BH=CK(hai cạnh tương ứng)
c) Ta có: ΔHBM=ΔKCN(cmt)
nên HM=KN(hai cạnh tương ứng)
Ta có: AH+HM=AM(H nằm giữa A và M)
AK+KN=AN(K nằm giữa A và N)
mà AM=AN(cmt)
và HM=KN(cmt)
nên AH=AK(đpcm)
d) Ta có: ΔHBM=ΔKCN(cmt)
nên \(\widehat{HBM}=\widehat{KCN}\)(hai góc tương ứng)
mà \(\widehat{OBC}=\widehat{HBM}\)(hai góc đối đỉnh)
và \(\widehat{OCB}=\widehat{KCN}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)

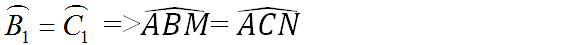
Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:
BM = CN (gt)
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)