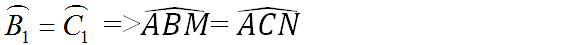Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: HB=HC=6cm
\(HA=\sqrt{10^2-6^2}=8\left(cm\right)\)
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO đo: ΔABM=ΔACN
Xét ΔBDM vuông tại D và ΔCEN vuông tại E có
BM=CN
\(\widehat{M}=\widehat{N}\)
Do đó: ΔBDM=ΔCEN
c: Xét ΔKBC có
KH là đường cao
KH là đường trung tuyến
Do đó:ΔKBC cân tại K
=>\(\widehat{KBC}=\widehat{KCB}\)
=>\(\widehat{KCB}=\widehat{DBM}\)
=>\(\widehat{KCB}=\widehat{ECN}\)
=>\(\widehat{KCB}+\widehat{BCE}=180^0\)
=>K,E,C thẳng hàng

a) Tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ACB}\)
Hay \(\widehat{ABD}=\widehat{ACE}\)
Theo định lý Cos ta có
\(AD=\sqrt{DB^2+AB^2-2\cdot DB\cdot AB\cdot\cos DBA}\)
\(AE=\sqrt{AC^2+CE^2-2\cdot AC\cdot CE\cdot\cos ACE}\)
Vì AB = AC ( tam giác ABC cân tại A ) và DB =CE và góc DBA = góc ACE
Nên AD = AE hay tam giác ADE cân tại A
b)\(\widehat{ADB}=\widehat{AEC}\)(ADE cân)
Nên góc KCE = góc DBH
Vậy \(\widehat{HBA}=\widehat{KCA}\)( góc DBA = góc ACE)
Xét tam giác HBA và tam giác ACK vuông có :
+ góc HBA = góc KCA
+ AB = AC
\(\Rightarrow\Delta HBA=\Delta KCA\left(ch-gn\right)\)=> HB = KC (hai cạnh tương ứng)
c) Ta có \(180^0=\widehat{HBA}+\widehat{ABC}+\widehat{OBC}\)
\(180^0=\widehat{ACK}+\widehat{ACB+\widehat{OCB}}\)
\(\widehat{HBA}=\widehat{ACK}\)
\(\widehat{ABC}=\widehat{ACB}\)
Nên \(\widehat{OCB}=\widehat{OBC}\)hay tam giâc OBC cân tại O
d) Xét tam giác AMB và tam giác AMC
+ AM chung
+ BM = MC (gt)
+ AB = AC (gt)
Vậy hai tam giác trên bằng nhau theo trường hợp c-c-c
Và hai góc BAM = góc CAM
Hay AM là tia phân giác của góc BAC
Xét tam giác AOB và tam giác ACO
+ AB = AC (gt)
+ OB = OC (cmt )
+ góc ABO = góc ACO vì \(\widehat{ABM+\widehat{OBC}=\widehat{ACM}+\widehat{OCB}}\)
Vậy hai tam giác trên bằng nhau theo trường hợp c-g-c
Và góc BAO = góc CAO
Hay AO là phân giác của góc BAC
Một góc chỉ có duy nhất một tia phân giác nên AM và AO là một hay A,M,O thẳng hàng

1
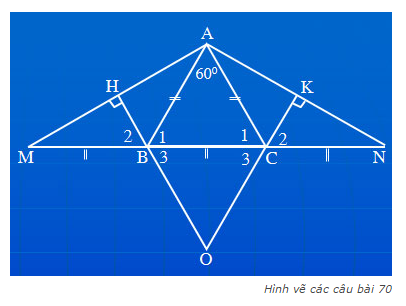
a) trước tiên chứng minh\(\widehat{ABM}=\widehat{ACN}\)
rồi mới chứng minh 2 tam giác ABM và ACN bằng nhau
suy ra AM = AN
b)Đầu tiên chứng minh\(\widehat{ABH}=\widehat{ACK}\)
rồi chứng minh hai tam giác ABH và ACK bằng nhau
suy ra BH = CK
c) vì hai tam giác ABH và ACK bằng nhau (cmt)
nên AH = AK
d) ta có \(\widehat{AMB}=\widehat{ACN}\)(hai tam giác ABH và ACK bằng nhau)
nên dễ cm \(\widehat{MBH}=\widehat{NCK}\)
còn lại tự cm
e) dễ cm tam giác ABC đều
vẽ \(BH\perp AC\)
nên BH vừa là đường cao; phân giác và trung tuyến
dễ cm \(\Delta BHC=\Delta NKC\)
nên \(\widehat{BCH}=\widehat{NCK}=60^0\)
từ đó dễ cm AMN cân và OBC dều

1) đề có phải là: Cho tam giác ABC cân tại A, góc A nhỏ hơn 90 độ. Vẽ BD vuông AC và CE vuông AB. H là giao điểm của BD và CE.
a) Chứng minh Tam giác ABD = Tam giác ACE
b) Chứng minh tam giác AED cân
c, AH là đường trung trực của ED.
D) Trên tia đối DB lấy K sao cho DK = DB. Chứng minh góc ECB = Góc DKC
A B C D E H K
a) Xét tam giác ABD và tam giác ACE có:
\(\widehat{ACE}=\widehat{ABD}\left(cùngphuvoi\widehat{BAC}\right)\Rightarrow\Delta ABD=\Delta ACE\left(g.c.g\right)\hept{\begin{cases}AC=AB\left(\Delta ABCcântạiA\right)\\\widehat{BAC}chung\\\widehat{AEC}=\widehat{ADB}=90^o\end{cases}}\)
b) AE=AD(vì tam giác ABD=tam giác ACE
=> tam giác AED cân tại A
c) Xem lại đề
d) Xét tam giác BCK có:
\(\hept{\begin{cases}BK\perp DC\\BD=DK\end{cases}}\)
=> CD là đường trung trực của BK
=> BC=CK
=> tam giác BCK cân tại C
=>\(\widehat{CBK}=\widehat{CKB}\)
Mà \(\widehat{ECB}=\widehat{CBK}\)(vì góc ABC=góc ACB; góc ABD= góc ACE)
=> góc ECB= góc CKB
3) Đề là:
Cho góc xOy, vẽ tia phân giác Ot của góc xOy. Trên tia Ot lấy điểm M bất kì, trên tia Ox và Oy lần lượt lấy các điểm A và B sao cho OA = OB gọi H là giao điểm của AB và Ot . CHỨNG MINH:
a/ MA = MB
b/ OM là đường trung trực của AB
c/ Cho biết AB = 6cm; OA= 5cm. Tính OH ? (bn viết khó hiểu qá nên mk xem lại trong vở)
Tự vẽ hình!
a/ Xét tam giác OAM và tam giác OBM, có:
Cạnh OM là cạnh chung
OA = OB (gt)
góc AOM = góc BOM ( vì Ot là tia phân giác của góc xOy)
=> Tam giác OAM = tam giác OBM (c.g.c)
=> MA = MB ( 2 cạnh tương ứng)
b/ Ta có: MA = MB (cmt)
=> Tam giác AMB là tam giác cân
=> Góc MAH = góc MBH
Xét tam giác AMH và tam giác BMH, có:
góc MAH = góc MBH ( cmt)
MA = MB ( cmt)
góc AMH = góc BMH ( vì tam giác OAM = tam giác OBM)
=> tam giác AMH và tam giác BMH ( g.c.g)
=> AH = HB ( 2 cạnh tương ứng)
=> H là trung điểm của AB (1)
Vì tam giác AMH = tam giác BMH (cmt)
=>góc MHA = góc MHB ( 2 góc tương ứng)
mà góc MHA + góc MHB = 180 độ ( 2 góc kề bù)
=> góc MHA = góc MHB= 180 độ : 2 = 90 độ
=> MH vuông góc với AB (2)
Từ (1) và (2)
=> MH là đường trung trực của AB
=> OM là đường trung trực của AB ( vì H thuộc OM )
c/ Vì H là trung điểm của AB (cmt)
=> AH =HB = AB : 2 = 6 :2 = 3 (cm)
Xét tam giác OAH vuông tại H có: OA2 = OH2 + AH2 ( định lí Py-ta-go)
=> 52 = OH2 + 32
=> 25 = OH2 + 9
=> OH2 = 25 - 9
=> OH2 = 16
\(\Rightarrow OH=\sqrt{16}\)
\(\Rightarrow OH=4cm\)