Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAMBΔAMBvà ΔAMCΔAMCcó :
AM ( cạnh chung )
AB = AC ( gt )
MB = MC ( gt )
Suy ra : ΔAMBΔAMB= ΔAMCΔAMC( c.c.c )
⇒⇒ˆAMB=ˆAMCAMB^=AMC^( hai cạnh tương ứng ) mà ˆAMB+ˆAMC=180oAMB^+AMC^=180o
⇒⇒ˆAMB=ˆAMC=ˆBMC2=90oAMB^=AMC^=BMC^2=90o⇒⇒AM ⊥⊥BC
b) Xét ΔADFΔADFvà ΔCDEΔCDEcó :
DE = DF ( gt )
ˆEDC=ˆFDAEDC^=FDA^( hai góc đối đỉnh )
DA = DC ( gt )
Suy ra : ΔADFΔADF= ΔCDEΔCDE( c.g.c )
⇒ˆFAD=ˆECD⇒FAD^=ECD^( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong nên AF // EC
c) gọi H là giao điểm của BD và AE
Xét ΔAHDΔAHDvuông tại H có : ˆHAD+ˆADH=90oHAD^+ADH^=90o( 1 )
Xét ΔBADΔBAD vuông tại A có : ˆABD+ˆBDA=90oABD^+BDA^=90o( 2 )
Từ ( 1 ) và ( 2 ) ⇒ˆHAD=ˆABD⇒HAD^=ABD^
Xét ΔBADΔBADvà ΔACGΔACGcó :
ˆDBA=ˆGACDBA^=GAC^( cmt )
AB = AC ( gt )
ˆBAD=ˆACGBAD^=ACG^( = 90o90o)
Suy ra : ΔBADΔBAD= ΔACGΔACG( g.c.g )
⇒AD=CG⇒AD=CG( hai cạnh tương ứng )
Mà AD=DC=AC2AD=DC=AC2
⇒CG=AC2=AB2⇒CG=AC2=AB2( vì AB = AC )
⇒AB=2CG

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

xét 2 tam giác ABM=tam giác ACM(c.c.c)(tự cm)
nên góc AMB=góc AMC=180ddooj /2=90 độ
suy ra AM vuông góc vs BC

A B C H D E F M K N
a/
\(BH\perp AC\Rightarrow HF\perp AC;ME\perp AC\) => ME//HF
\(AC\perp AB\Rightarrow EH\perp HF;MF\perp BH\Rightarrow MF\perp HF\) => EH//MF
=> MEHF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => ME=HF (cạnh đối hbh)
b/
\(\widehat{BMD}+\widehat{ABC}=90^o\)
\(\widehat{CME}+\widehat{ACB}=90^o\)
\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân)
\(\Rightarrow\widehat{BMD}=\widehat{CME}\)
Mà \(\widehat{CME}=\widehat{CBH}\) (góc đồng vị)
\(\Rightarrow\widehat{BMD}=\widehat{CBH}\)
Xét tg vuông DBM và tg vuông FMB có
\(\widehat{BMD}=\widehat{CBH}\)
BM chung
=> tg DBM = tg FMB (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
c/
Ta có ME = HF (cmt)
tg DBM = tg FMB (cmt) => MD = BF
=> MD+ME=BF+HF=BH không đổi
d/
Từ D dựng đt // AC cắt BC tại N
\(\Rightarrow\widehat{BND}=\widehat{ACB}\) Góc đồng vị)
\(\widehat{ABC}=\widehat{ACB}\)
=> \(\widehat{BND}=\widehat{ABC}\) => tg DBN cân tại D => BD=ND (1)
tg DBM = tg FMB (cmt) => BD=MF (2)
Mà MF = EH (cạnh đối hbh) (3)
Mà EH = KC (4)
Từ (1) (2) (3) (4) => ND = KC
Mà ND//AC => ND//KC
=> DEKN là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)
Mà DK và NC là hai đường chéo của hbh cắt nhau tại trung điểm mỗi đường => trung điểm của KD nằm trên NC mà NC thuộc BC => trung điểm KD nằm trên BC
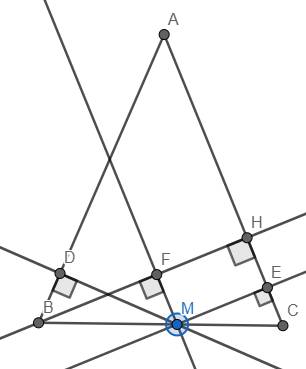
a) Vẽ MH, rõ ràng HEMF có tổng số đo của 4 góc là 360o (vì tổng số đo của 4 góc đó là tổng số đo của các góc của các tam giác FMH và EMH)
Mà theo giả thuyết \(MD\perp AB\), \(ME\perp AC\) và \(MF\perp BH\) nên \(MF\perp ME\). Suy ra HEMF là hình chữ nhật, từ đó ME = HF.
b) Ta có \(\widehat{ABM}=\widehat{ACM}\) (vì tam giác ABC cân tại A) và \(\widehat{FMB}=\widehat{ACM}\) (vì hai góc đồng vị và AC//MF vì \(ME\perp AC\) và \(MF\perp ME\)), suy ra \(\widehat{ABM}=\widehat{FMB}\).
Xét tam giác DBM vuông tại D và FMB vuông tại F có BM là cạnh chung và \(\widehat{ABM}=\widehat{FMB}\), suy ra ΔDBM = ΔFMB (cạnh huyền - góc nhọn)
c) Từ a) và b) suy ra MD = BF, MD + ME = BF + FH = BH. Vậy khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.
Bài này cũng tương đối dễ, mk sẽ gợi ý sơ sơ cho bạn !
Kẻ \(BH\perp AC;MI\perp BH\)
△ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\)
Vì \(HC\perp BH;MI\perp BH\Rightarrow HC//MI\\ \Rightarrow\widehat{IMB}=\widehat{ACB}\left(haigócđồngvị\right)\)
Xét △BEM=△MIB(ch - gn )
⇒ME = BI ( hai cạnh tương ứng )(1)
Ta có : HI = MF ( t/c đoạn chắn )(2)
Từ (1) và (2) ⇒ME + MF = BI + HI = BH
⇒Đpcm