Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tam giác AIH và tam giác HIC đều vuông tại I
tam giác ABC cân tại A ; H là trung điểm của BC (gt)
=> AH _|_ BC (đl) và AH là phân giác của góc BAC
=> góc BAH + góc ABC = 90 mà góc ABH = góc HAC
=> góc HAC + góc ABC = 90
tam giác ABC cân tại A => góc B = Góc C
có góc IHC + góc ACB = 90
=> gócIHC + góc ABC = 90
=> góc HAC = góc IHC
tam giác AIH và tam giác HIC đều vuông tại I
=>t am giác AIH ~ tam giác HIC
=> HA/HC = HI/IC
=> HA.IC = HC.HI

A B C M H N I E Q K D
a/
\(BN\perp AC;MH\perp AC\) => MH//BN
Xét tg BNC có
MH//BN
MB=MC
=> HN=HC (trong tg đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
MH//BN. Xét tg AMH
\(\dfrac{ED}{IM}=\dfrac{EN}{IH}\) (talet)
Mà IM=IH => ED=EN
b/
Xét tg vuông ABN có
\(BN^2=AB^2-AN^2=AC^2-AN^2=\)
\(=AC^2-\left(AC-CN\right)^2=AC^2-\left(AC-2HN\right)^2=\)
\(=AC^2-AC^2+4AC.HN-4HN^2=\)
\(=4HN.\left(AC-HN\right)=4HN\left(AC-HC\right)=\)
\(=4HN.HA\)
Xét tg BCN có
MB=MC; HN=HC => MH là đường trung bình => \(MH=\dfrac{BN}{2}\)
Mà MH=2MI\(\Rightarrow2MI=\dfrac{BN}{2}\Rightarrow BN=4MI\)
Ta có
\(BN^2=4HN.HA\Rightarrow\left(4MI\right)^2=4HN.HA\)
\(\Rightarrow16MI^2=4.HN.HA\Rightarrow MI^2=HN.HA\)

A B C M N H
a) Ta có: góc MNC = góc BAC = 900
=> MN // BC (2 góc đồng vị bằng nhau) (đpcm)
b) Ta có: AC // HM (gt)
Và AC vuông góc với AB (góc BAC = 900)
=> MH vuông góc với AB (đpcm)
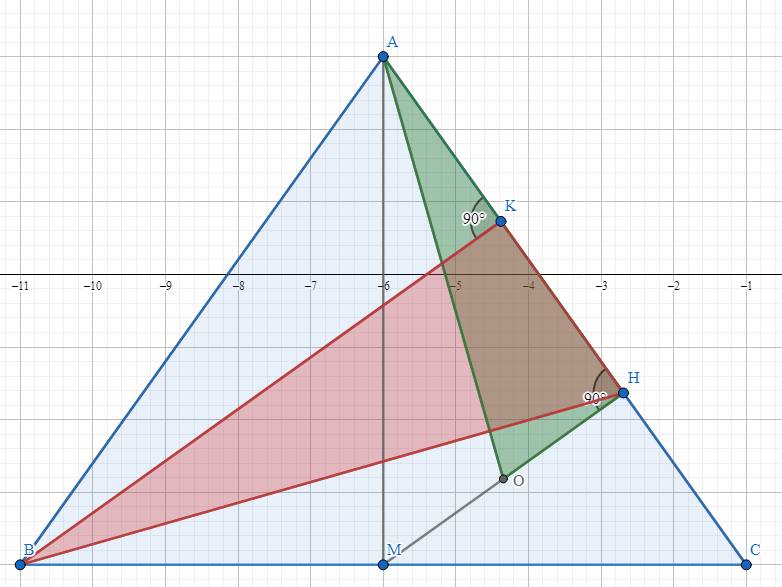
Xét tam giác \(AMH\) và tam giác \(BCK\):
\(\widehat{MAH}=\widehat{CBK}\) (vì cùng phụ với góc \(\widehat{ACM}\))
\(\widehat{AHM}=\widehat{BKC}\left(=90^o\right)\)
suy ra \(\Delta AMH\sim\Delta BCK\left(g.g\right)\)
\(\Rightarrow\dfrac{MH}{AH}=\dfrac{CK}{BK}\Rightarrow\dfrac{OH}{AH}=\dfrac{HK}{BK}\)
\(\Rightarrow\Delta AOH\sim\Delta BHK\left(c.g.c\right)\)
Gọi giao điểm \(BK\) và \(AO\) là \(P\), giao điểm \(AO\) và \(BH\) là \(Q\).
\(BK//MH\) suy ra \(\widehat{APK}=\widehat{AOH}\) mà \(\widehat{AOH}=\widehat{BHK}\) và \(\widehat{APK}+\widehat{QPK}=180^o\)
suy ra \(\widehat{QPK}+\widehat{QHK}=180^o\) suy ra \(\widehat{PQH}+\widehat{PKH}=180^o\)
suy ra \(\widehat{PQH}=90^o\)
do đó ta có đpcm.
\(\dfrac{MH}{AH}=\dfrac{CK}{BK}\Rightarrow\dfrac{OH}{AH}=\dfrac{HK}{BK}\)
Có thể gải thích lại chỗ này được không ạ?