Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H D E K I
a/
Ta có
\(AB\perp AC\Rightarrow AD\perp AC;HE\perp AC\) => AD//HE
\(AC\perp AB\Rightarrow AE\perp AB,HD\perp AB\) => AE//HD
=> ADHE là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> ADHE là hình CN
b/
Xét tg vuông ADH có
\(DH=\sqrt{AH^2-AD^2}\) (Pitago)
\(\Rightarrow DH=\sqrt{5^2-4^2}=3cm\)
\(\Rightarrow S_{ADHE}=AD.DH=4.3=12cm^2\)
c/
Ta có
DB=DI (gt); DH=DK (gt) => BKIH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Xét tg AKH có
\(HD\perp AB\Rightarrow AD\perp HK\) (1)
BKIH là hình bình hành (cmt) => KI//BH (cạn đối hbh)
Mà \(AH\perp BC\left(gt\right)\Rightarrow BH\perp AH\)
\(\Rightarrow KI\perp AH\) (2)
Từ (1) và (2) => I là trực tâm của tg AKH => \(AK\perp HI\) (trong tg 3 đường cao đồng quy)

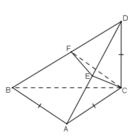
MH =\(\sqrt{2}a\) => MC = \(2\sqrt{2}a\) và CH = \(\sqrt{6}a\)
=> BC = 2CH = \(2\sqrt{6}a\)
=> AC = BC = \(2\sqrt{6}a\)
Tam giác DBC vuông cân tại D => DH = HB = HC = \(\sqrt{6}a\) => DC = \(\sqrt{12}a\)
Tam giác MDC vuông tại M => MD2 = DC2 - MC2 = 12a2 - 8a2 = 4a2 => MD = 2a
Tam giác MAC vuông tại M => MA2 = AC2 - MC2 = 24a2 - 8a2 = 16a2 => MA = 4a
Trong mặt phẳng BCD, điểm H cách đều B, C, D => Hình cầu ngoại tiếp ABCD nằm trên đường thẳng đi qua H và vuông góc với mặt phẳng BCD. Đường thẳng này nằm trong mặt phẳng HDA (Vì đường thẳng đó vuông góc với BC nên sẽ nằm trên mặt phẳng HDA).
Đồng thời tâm hình cầu cách đều A và D => Tâm đó nằm trên đường trung trực của AD trong mặt phẳng HDA.
Ta vẽ riêng tam giác HDA ra, kẻ đường HE vuông góc với HD cắt AD tại E. Ta có HM là đường cao tam giác vuông HED nên:
HD2 = MD.DE => 6a2 = 2a. DE => DE = 3a.
Mà AD = MD + DA = 2a + 4a = 6a => AE = AD - DE = 6a -3a = 3a => Điểm E là điểm giữa của A và D.
Vậy E chính là tâm hình cầu ngoại tiếp tứ diện ABCD, bán kính hình cầu là ED = 3a => Thể tích khối cầu ....

S A B H C
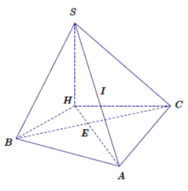
Tam giác ABC vuông cân tại A nên \(BC=2AH=2a\)
Từ đó \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}a.2a=a^2\)
Vì \(SA\perp\left(ABC\right);AH\perp BC\) suy ra \(SH\perp BC\)
Do đó : \(\left(\left(SBC\right),\right)\left(ABC\right)=\widehat{SHA}=60^0\)
Suy ra \(SA=AH.\tan60^0=a\sqrt{3}\)
Vậy \(V_{SABC}=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}a\sqrt{3}a^2=\frac{a^3\sqrt{3}}{3}\)

Câu 2: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3(câu này ko bt,thông cảm)
B. -1 và -3
C. 1 và -3
D. -1 và -3i.(câu này ko rõ)
Câu 3: Môđun của số phức z thỏa mãn z− = 8 - 6i là
A. 2
B. 10
C. 14
D. 2√7
Câu 4: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
A. x = 3, y = 1
B. x = 3, y = -1
C. x = -3, y = -1
D. x = -3, y = 1

Sắp tới tháng cô hồn rồi. Ai cũng biết tháng cô hồn rất xui. Vì vậy ai đọc được cái này thì gửi cho đủ 30 người. Vì lúc trước có cô gái đọc xong không gửi, 2 ngày sau khi đi tắm cô ấy bị ma cắn cổ mà chết và mẹ cô ấy cũng chết. 2 vợ chồng kia đọc xong liền gửi đủ 30 người, hôm sau họ trúng số. Nên bạn phải gửi nhanh!!!!!!!...\\n



giup em voi
Hình Thang cân
Ta có: tam giác ABC là tam giác cân tại A.
=> góc B= góc C
Vì BD và CE là phân giác góc B và C
=> góc DBC = góc EBD = góc DCE = góc ECB
Xét tam giác EBC và tam giác DBC có:
góc ECB = góc DBC
góc BCD = góc EBC
Chung cạnh BC