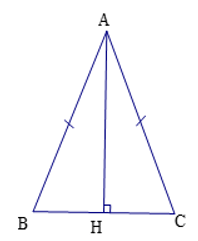
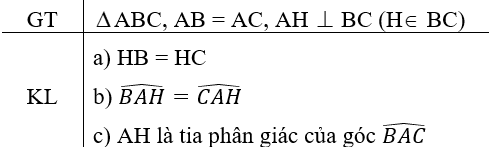
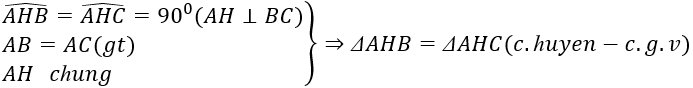Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
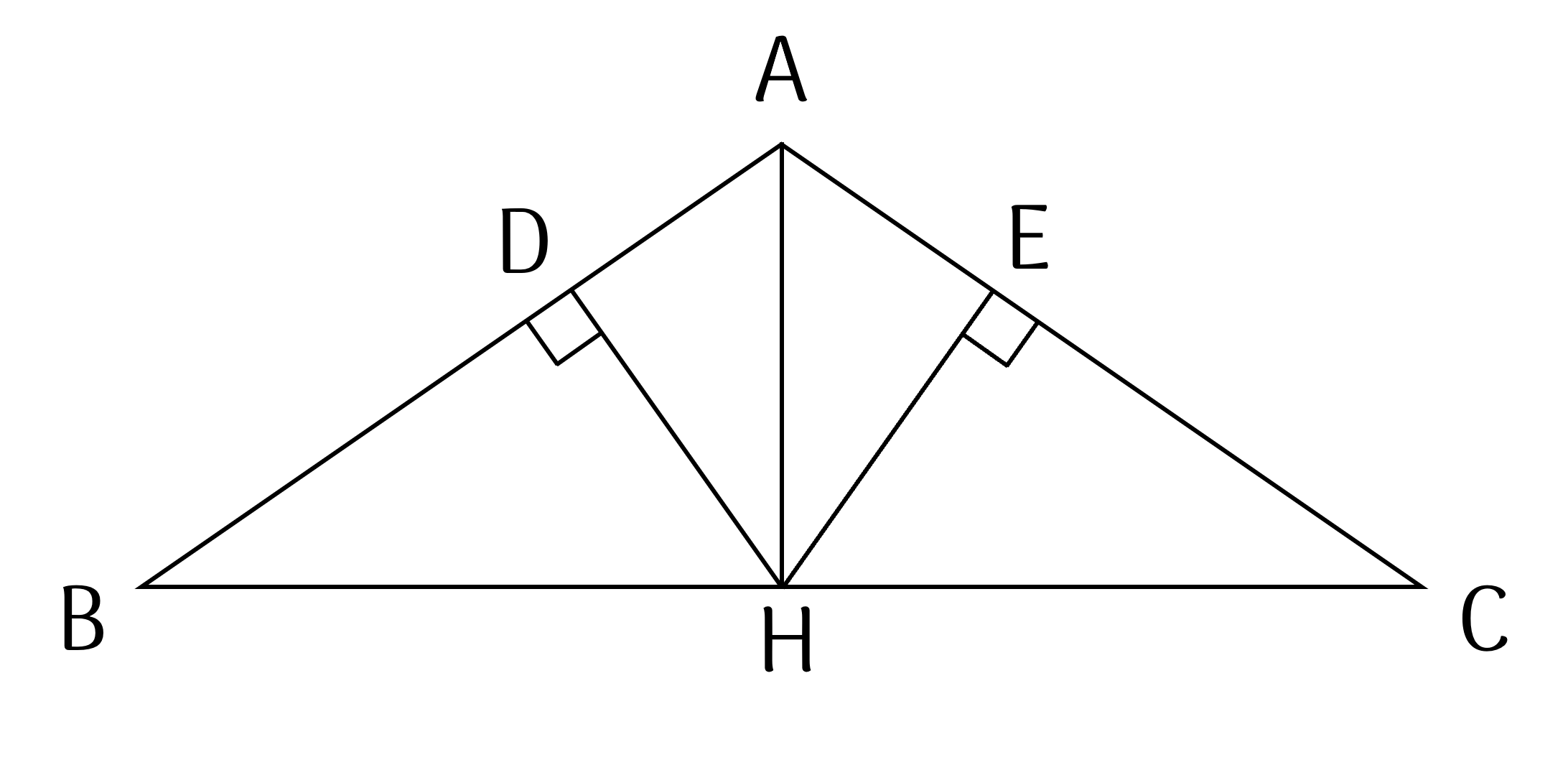
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểmcủa BC
hay HB=HC
b: Xét ΔADH vuông tạiD và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra HD=HE
hay ΔHDE cân tại H

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H

a) Chứng minh HB=HC: Xét ΔAHB và ΔAHC có: ∠AHB=∠AHC=90(độ) AH cạnh chung AB=AC(gt) ⇒ ΔAHB = ΔAHC (ch-cgv) ⇒ HB=HC (2 cạnh tương ứng)
b) Ta có: HB=HC=BC/2=6/2=3(cm) Ta có: ΔAHB vuông tại H. ⇒ AH(mũ 2)+BH(mũ 2)=AB(mũ 2) ⇒ AH(mũ 2)=AB(mũ 2)-BH(mũ 2) =4(mũ 2)-3(mũ 2)=16-9=7 ⇒ AH=√7(cm)
c) Ta có: ΔAHB = ΔAHC ⇒ ∠BAH=∠CAH Xét ΔAHD và ΔAHE có: ∠D=∠E=90(độ) AH cạnh chung ∠BAH=∠CAH (gt) ⇒ ΔAHD = ΔAHE (ch-gn) ⇒ DH=EH ⇒ ΔHDE cân tại H. A B C H D E

b) Xét ΔBAH vuông tại H và ΔCAH vuông tại H có
BA=CA(ΔBAC cân tại A)
AH chung
Do đó: ΔBAH=ΔCAH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
Xét ΔDHB vuông tại D và ΔEHC vuông tại E có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔDHB=ΔEHC(Cạnh huyền-góc nhọn)
Suy ra: HD=HE(Hai cạnh tương ứng)
Xét ΔHDE có HD=HE(cmt)
nên ΔHDE cân tại H(Định nghĩa tam giác cân)