Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: (bạn tự vẽ hình nhé)
a) Xét \(\Delta\)BAH và \(\Delta\)CAH :
AHB^ = AHC^ = 90o
AB = AC
ABH^ = ACH^
=> \(\Delta\)BAH = \(\Delta\)CAH (cạnh huyền _ góc nhọn) (2)
=> BH = CH (2 cạnh tương ứng) (1)
Mà BH + CH = BC
<=> 2 * BH = 6
BH = 3 (cm)
ABH^ = ACH^
Áp dụng định lý Py-ta-go vào \(\Delta\)ABH:
BH^2 + AH^2 = AB^2
AH^2 = AB^2 - BH^2 = 5^2 - 3^2 = 25 - 9 = 16 (cm)
\(\Rightarrow AH=\sqrt{16}=4\left(cm\right)\)
b) Từ (1) => AH là đường trung tuyến của \(\Delta\)BAC
=> A, G, H thẳng hàng.
c) Từ (2) => BAH^ = CAH^ hay BAG^ = CAG^
Xét \(\Delta\)BAG và \(\Delta\)CAG:
AB = AC
BAG^ = CAG^
AG chung
=> \(\Delta\)BAG = \(\Delta\)CAG (c.g.c)
=> ABG^ = ACG^ (2 góc tương ứng)

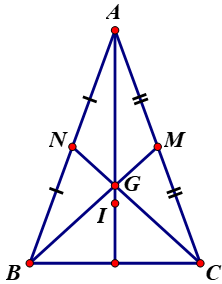
a, Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = 1/2BM; GC = 2/3CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> ˆBAG=ˆCAG => G thuộc phân giác của ˆBAC
Mà ∆ABI = ∆ACI (c.c.c)
=> ˆBAI=ˆCAI => I thuộc phân giác của ˆBAC
Vì G, I cùng thuộc phân giác của ˆBAC nên A, G, I thẳng hàng

a: Vì G là trọng tâm nên AG là đường trung tuyến ứng với BC
mà ΔABC cân tại A
nên AG là đường trung trực của BC(1)
I cách đều ba cạnh nên AI là phân giác của góc BAC
=>AI là trung trực của BC(2)
Từ (1) và (2) suy ra A,G,I thẳng hàng
c: Xét ΔIBG và ΔICG có
IB=IC
BG=CG
IG chung
Do đó; ΔIBG=ΔICG
Suy ra: góc IBG=góc ICG

a: Ta có: ΔABC cân tại A
mà AG là đường trung tuyến
nên AG là đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,G,I thẳng hàng
c: Xét ΔIBG và ΔICG có
IB=IC
BG=CG
IG chung
Do đó ΔIBG=ΔICG
Suy ra: góc IBG=góc ICG

Giải
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà \(GB=\frac{2}{3}BM;GC=\frac{2}{3}CN\)(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\)( hai góc tương ứng )
\(\Rightarrow\)G là trọng tâm của \(\widehat{BAC}\)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc tia phân giác của \(\widehat{BAC}\)nên A, G, I thẳng hàng