Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ nha bạn
a) Vì E và F lần lượt là trung điểm của AB và AC
\(\Rightarrow\)AE=EB và AF=FC
Vì tam giác ABC cân tại A nên AB=AC
\(\Rightarrow\)\(\frac{1}{2}AB=\frac{1}{2}AC\Rightarrow AE=AF;EB=FC\)
Xét tam giác AFB và tam giác AEC có:
AF=AE(chứng minh trên)
\(\widehat{A}\)chung
AB=AC(gt)
\(\Rightarrow\)tam giác AFB=tam giác AFC(c-g-c)
=> FB=EC(2 cạnh tương ứng)
b) Vì F là trung điểm của AC nên BF là trung tuyến của tam giác ABC tại đỉnh B
Vì E là trung điểm của AB nên CE là trung tuyến của tam giác ABC tại đỉnh C
Vì FB=EC(chứng minh trên)
=> \(BG=\frac{2}{3}BF=\frac{2}{3}CE=CG\)
=> tam giác BGC cân tại G
c) Vì AE=AF(chứng minh trên)
\(\Rightarrow\)tam giác AEF cân tại A
\(\Rightarrow\widehat{AFE}=\frac{180^0-\widehat{A}}{2}\)(1)
Tam giác ABC cân tại A
\(\Rightarrow\widehat{ACB}=\frac{\left(180^0-\widehat{A}\right)}{2}\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{AFE}=\widehat{ACB}\)
Mà 2 góc này ở vị trí đồng vị \(\Rightarrow\)EF//BC

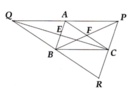
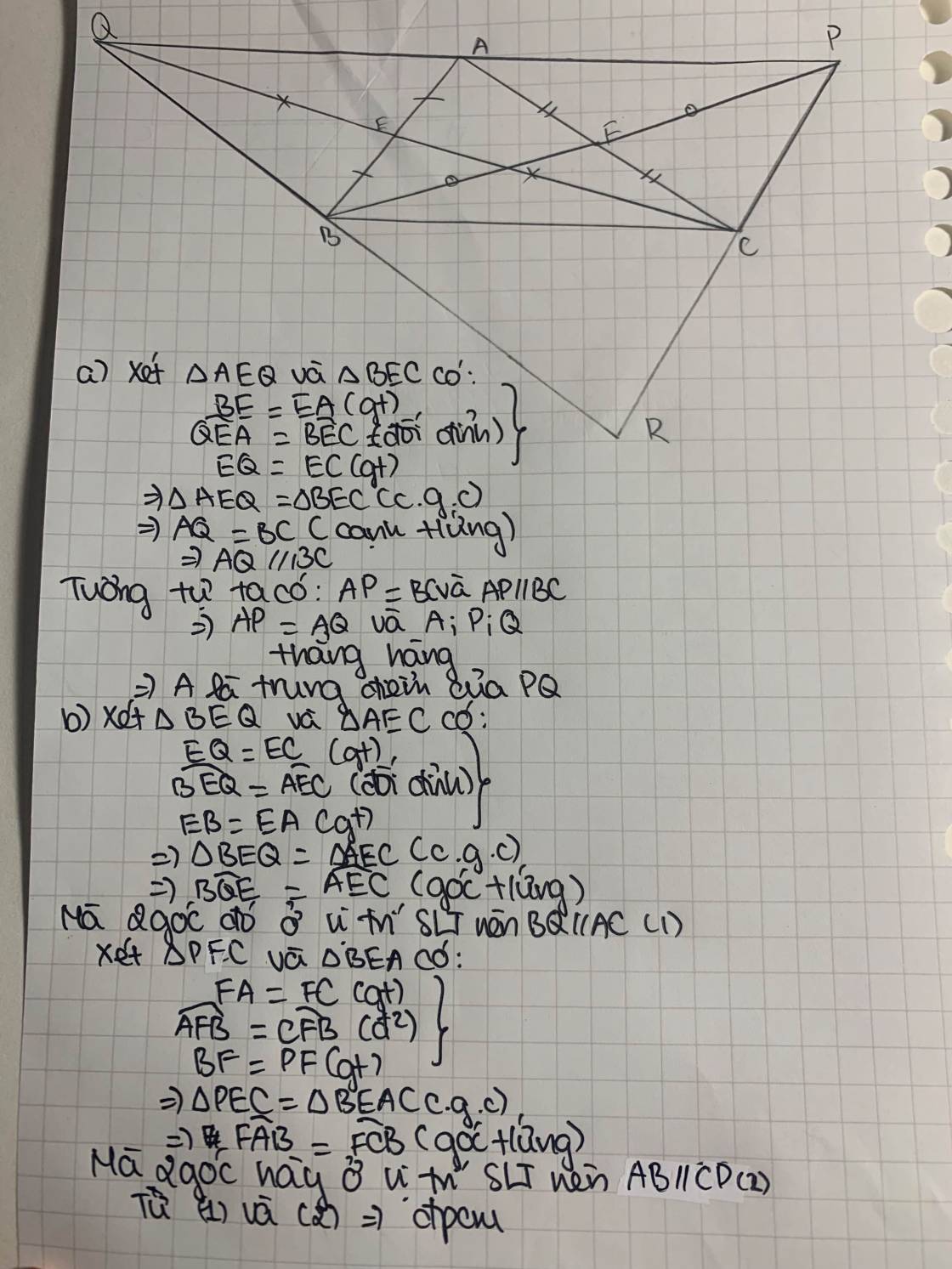
a) Xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=> tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
b: Ta có: ΔADB=ΔAEC
nên BD=CE
Xét ΔEBC vuông tạiE và ΔDCB vuông tại D có
BC chung
CE=BD
Do đó:ΔEBC=ΔDCB
Suy ra: \(\widehat{OCB}=\widehat{OBC}\)
hay ΔOBC cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: Ta có: ΔEBC vuông tại E
mà EM là đường trung tuyến
nên BC=2EM
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
ˆBADBAD^ chung
Do đó: ΔADB=ΔAEC
b: Ta có: ΔADB=ΔAEC
nên BD=CE
Xét ΔEBC vuông tạiE và ΔDCB vuông tại D có
BC chung
CE=BD
Do đó:ΔEBC=ΔDCB
Suy ra: ˆOCB=ˆOBCOCB^=OBC^
hay ΔOBC cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: Ta có: ΔEBC vuông tại E
mà EM là đường trung tuyến
nên BC=2EM


a: Xét ΔAFB và ΔAEC có
AF=AE
góc BAF chung
AB=AC
Do đo: ΔAFB=ΔAEC
Suy ra FB=EC
b: Xét ΔGCB có góc GCB=góc GBC
nên ΔGBC cân tại G
c: Xét ΔABC có AE/AB=AF/AC
nên FE//BC