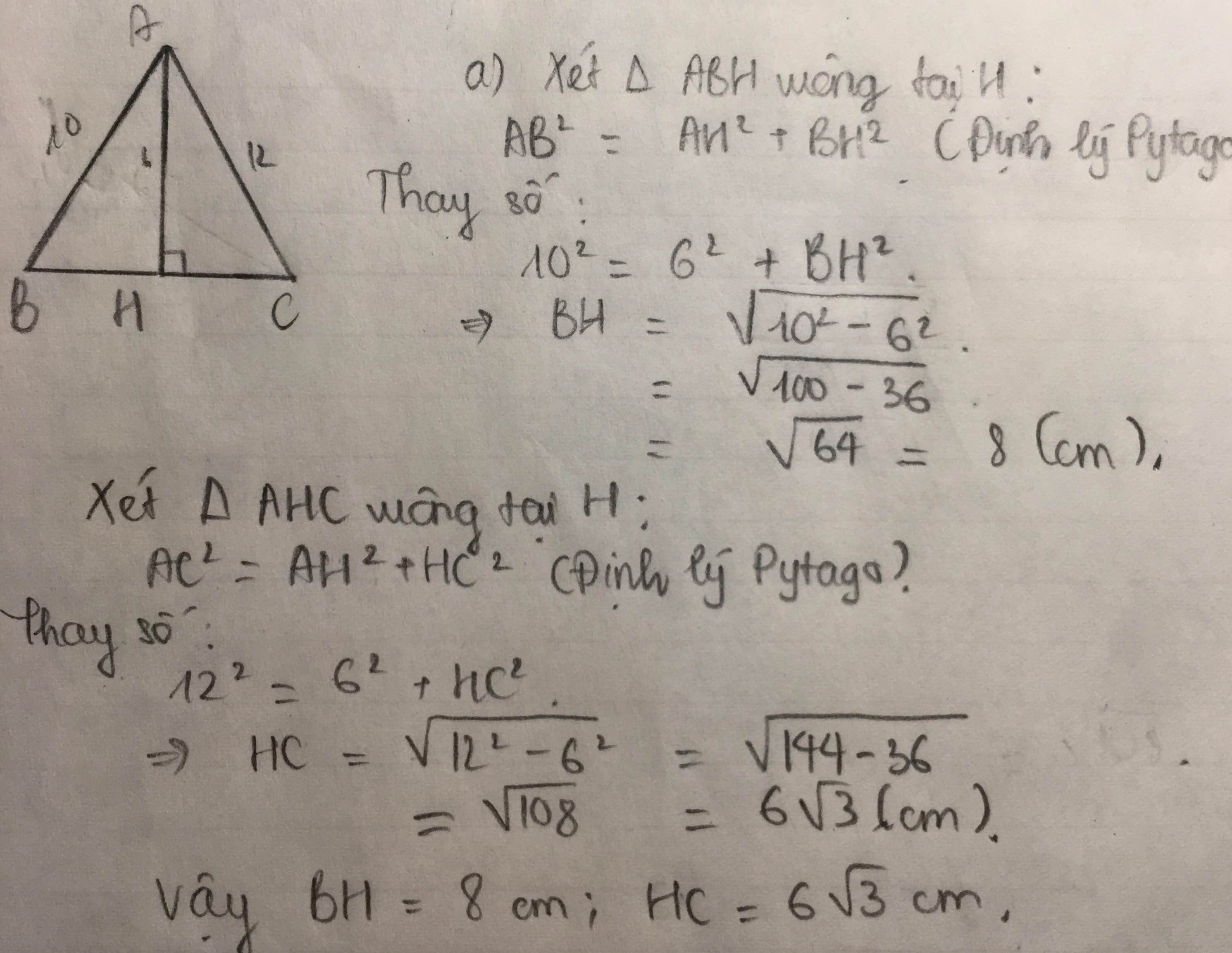Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

a) Xét ΔABHΔABH và ΔHACΔHAC có
AB=AC;ˆBAH=ˆCAH;AH:chungAB=AC;BAH^=CAH^;AH:chung
⇒⇒ ΔABHΔABH = ΔHACΔHAC (cgc)
b) Có BK = AB ⇒ΔABK⇒ΔABK cân tại B

a: Ta có: ΔABC cân tại A
mà AD là đường phân giác ứng với cạnh đáy BC
nên AD là đường cao ứng với cạnh BC
Xét ΔABC có
AD là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: CH\(\perp\)AB
Cảm ơn bạn!
Nhưng mình biết làm câu a với b rồi bạn làm cho mình câu c với d với