Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.

Chọn D.
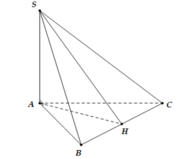
+) Ta có :
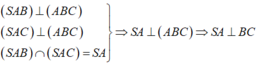
⇒ Suy ra : A đúng.
+) Ta có : 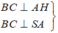
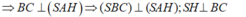
⇒ Suy ra : C đúng.
+) Mặt khác : AH ⊥ CD nên:
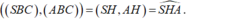
⇒ Suy ra : D sai.



Ta có : A' là h/c của A lên (P) ; BC \(\subset\left(P\right)\) \(\Rightarrow\) \(AA'\perp BC\)
Mà : \(AH\perp BC\) Suy ra : \(BC\perp\left(AA'H\right)\Rightarrow BC\perp A'H\)
Chỉ ra : \(\left(\left(P\right);\left(ABC\right)\right)=\widehat{A'HA}=30^o\)
\(\Delta A'HA\perp\) tại A : \(\dfrac{AH}{A'H}=cos30^o\Rightarrow A'H=\dfrac{\sqrt{3}}{2}.a\sqrt{3}=\dfrac{3a}{2}\)
\(S_{\Delta A'BC}=\dfrac{1}{2}.A'H.BC=\dfrac{1}{2}\dfrac{3a}{2}.3a=\dfrac{9a^2}{4}\)
Sửa lại : \(A'H=2a\)
\(S_{\Delta A'BC}=3a^2\)