Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
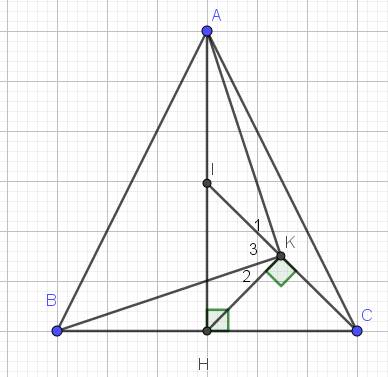
Vì $ABC$ cân tại $A$ nên đường cao $AH$ đồng thời là đường trung tuyến. Hay $H$ là trung điểm $BC$.
Xét tam giác $IHK$ và $HCK$ có:
$\widehat{IHK}=\widehat{HCK}$ (cùng phụ $\widehat{KHC}$)
$\widehat{IKH}=\widehat{HKC}=90^0$
$\Rightarrow \triangle IHK\sim \triangle HCK$ (g.g)
$\Rightarrow \frac{IH}{HK}=\frac{HC}{CK}$
$\Rightarrow \frac{2IH}{HK}=\frac{2HC}{CK}$
$\Rightarrow \frac{AH}{HK}=\frac{BC}{CK}$
Xét tam giác $BKC$ và $AKH$ có:
$\widehat{BCK}=\widehat{AHK}$ (cùng phụ với góc $\widehat{KHC}$)
$\frac{BC}{KC}=\frac{AH}{HK}$ (cmt)
$\Rightarrow \triangle BKC\sim \triangle AKH$ (c.g.c)
$\Rightarrow \widehat{BKC}=\widehat{AKH}$
$\Rightarrow \widehat{K_2}+90^0=\widehat{K_1}+90^0$
$\Rightarrow \widehat{K_2}=\widehat{K_1}$
$\Rightarrow \widehat{K_2}+\widehat{K_3}=\widehat{K_1}+\widehat{K_3}$
$\Rightarrow \widehat{IKH}=\widehat{AKB}$
Hay $90^0=\widehat{AKB}$

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
hay AH=DE

Ta có : DM = MC
DI = IH
=> MI là đường trung bình của tam giác vuông MCH
=> MI // HC
Do HC vuông vs AH => MI vuông vs AH ( đpcm )

\(a,\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\\ \Rightarrow AEHD\text{ là hcn}\\ \Rightarrow AH=DE\\ b,DI\text{ là tt ứng cạnh huyền }BH\Rightarrow DI=IH\Rightarrow\widehat{IDH}=\widehat{IHD}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{EDH}=\widehat{AHD}\\ \Rightarrow\widehat{IDE}=\widehat{IDH}+\widehat{EDH}=\widehat{IHD}+\widehat{AHD}=\widehat{IHA}=90^0\\ \Rightarrow DI\perp DE\left(1\right)\\ EK\text{ là tt ứng cạnh huyền }CH\Rightarrow EK=KH\Rightarrow\widehat{KEH}=\widehat{KHE}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{AHE}=\widehat{DEH}\\ \Rightarrow\widehat{DEK}=\widehat{DEH}+\widehat{HEK}=\widehat{AHE}+\widehat{KHE}=\widehat{AHK}=90^0\\ \Rightarrow EK\perp DE\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI\text{//}EK\)

a) Xét tứ giác AMHN có
\(\widehat{NAM}=90^0\)(\(\widehat{BAC}=90^0\), M∈AB, N∈AC)
\(\widehat{ANH}=90^0\)(HN⊥AC)
\(\widehat{AMH}=90^0\)(HM⊥AB)
Do đó: AMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)