Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/ Xét ΔABM;ΔACMΔABM;ΔACM có :
⎧⎩⎨⎪⎪AB=ACBˆ=CˆMB=MC{AB=ACB^=C^MB=MC
⇔ΔAMB=ΔAMC(c−g−c)⇔ΔAMB=ΔAMC(c−g−c)
b/ Xét ΔBHM;ΔCKMΔBHM;ΔCKM có :
⎧⎩⎨⎪⎪⎪⎪BHMˆ=CKMˆ=900Bˆ=CˆMB=MC{BHM^=CKM^=900B^=C^MB=MC
⇔ΔBHM=ΔCKM(ch−gn)⇔ΔBHM=ΔCKM(ch−gn)
⇔BH=CK
a, xet tam giac ABM va tam giac ACM co
AB = AC ( tam giac ABC can)
goc ABM = goc ACM (tam giac ABC can)
BM = MC ( AM la duong trung tuyen)
suy ra tam giac ABM = tam giac ACM (c.g.c)
b,ta co BM=MC=1/2BC
suy ra BM = 1/2.6=3
ta co AM = AB + BM = 5+3 = 8
Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
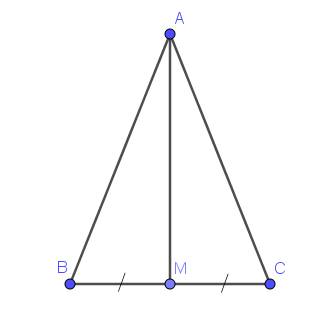
là sao