Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

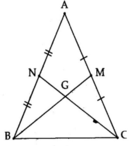
Xét △AMB và △ANC ta có:
AM=AN ( Vì M,N lần lượt là trung điểm của 2 cạnh AB, AC)
\(\widehat{A}\) là góc chung
AB=AC (Vì là hai cạnh bên trong tam giác cân)
\(\Rightarrow\Delta AMB=\Delta ANC\left(c-g-c\right)\)
\(\Rightarrow BM=CN\) (hai cạnh tương ứng)
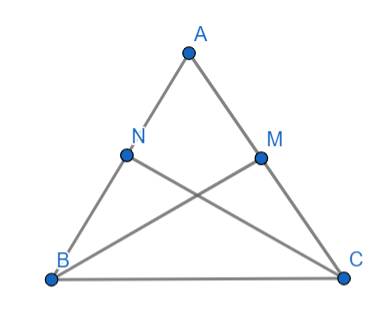
Xét ΔAMB và ΔANC có
AM=AN
góc A chug
AB=AC
=>ΔAMB=ΔANC
=>BM=CN

a)
ta có: AB=AC suy ra 1/2 AB=1/2AC suy ra AN=NB=AM=MC
xét tam giác ABM và tam giác ACN có:
AB=AC
AM=AN(cmt)
A(chung)
suy ra tam giác ABM=ACN(c.g.c)
suy ra BM=CN
b)
ta có: I là trọng tâm cua tam giác ABC
ta có: MB=NC(theo câu a) suy ra 2/3MB=2/3NC suy ra IB=IC suy ra tam giac IBC cân tại I
c)
xét tam giác AIB và tam giác AIC có:
AB=AC
AI(chung)
IB=IC
suy ra tam giác AIB=AIC(c.c.c)
suy ra BAI=CAI
suy ra AI là phân giác của góc A

Tham khảo:
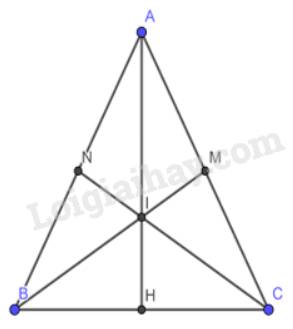
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC

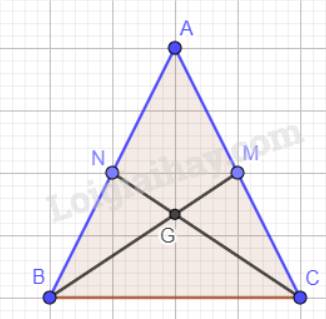
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.