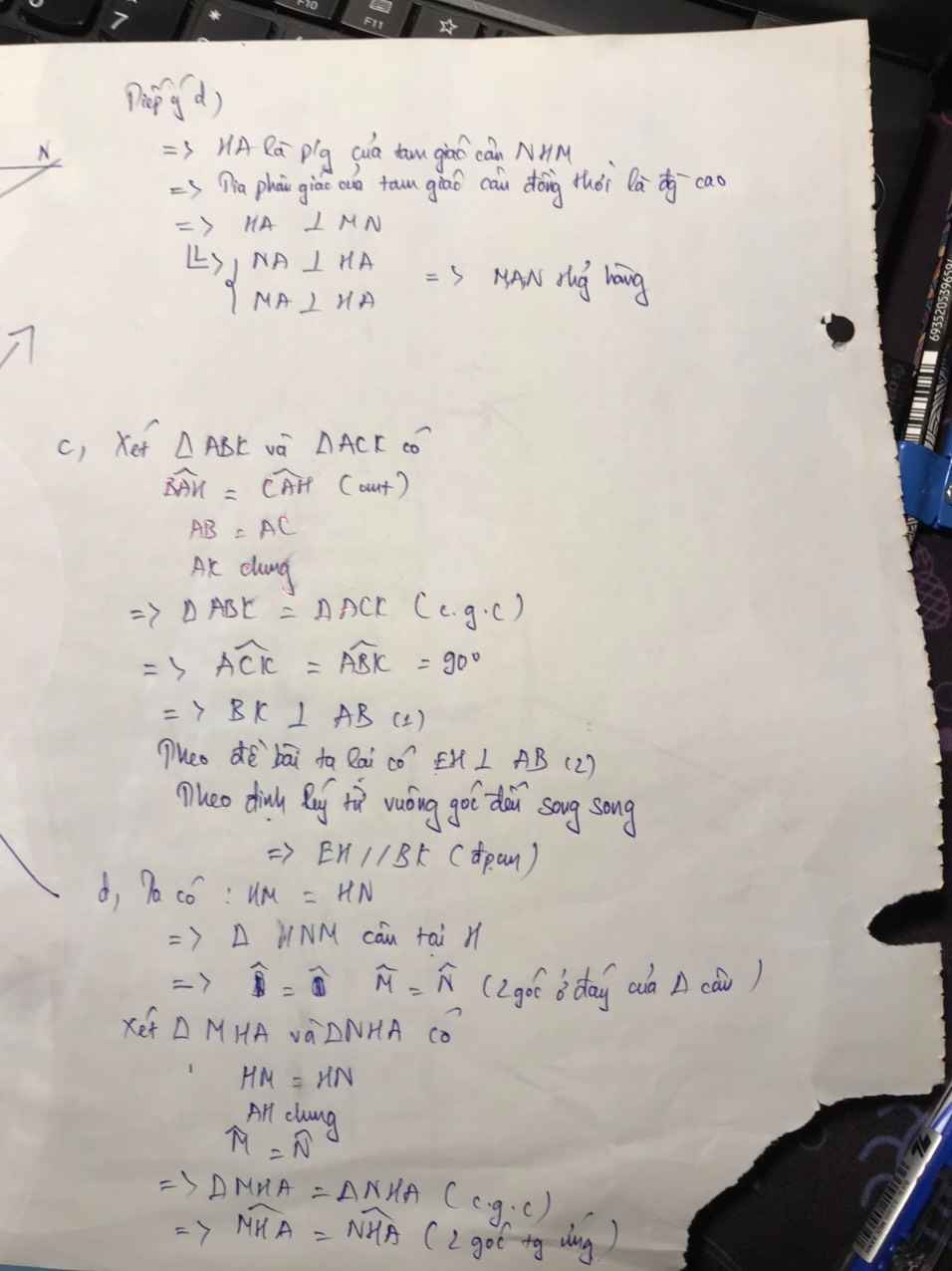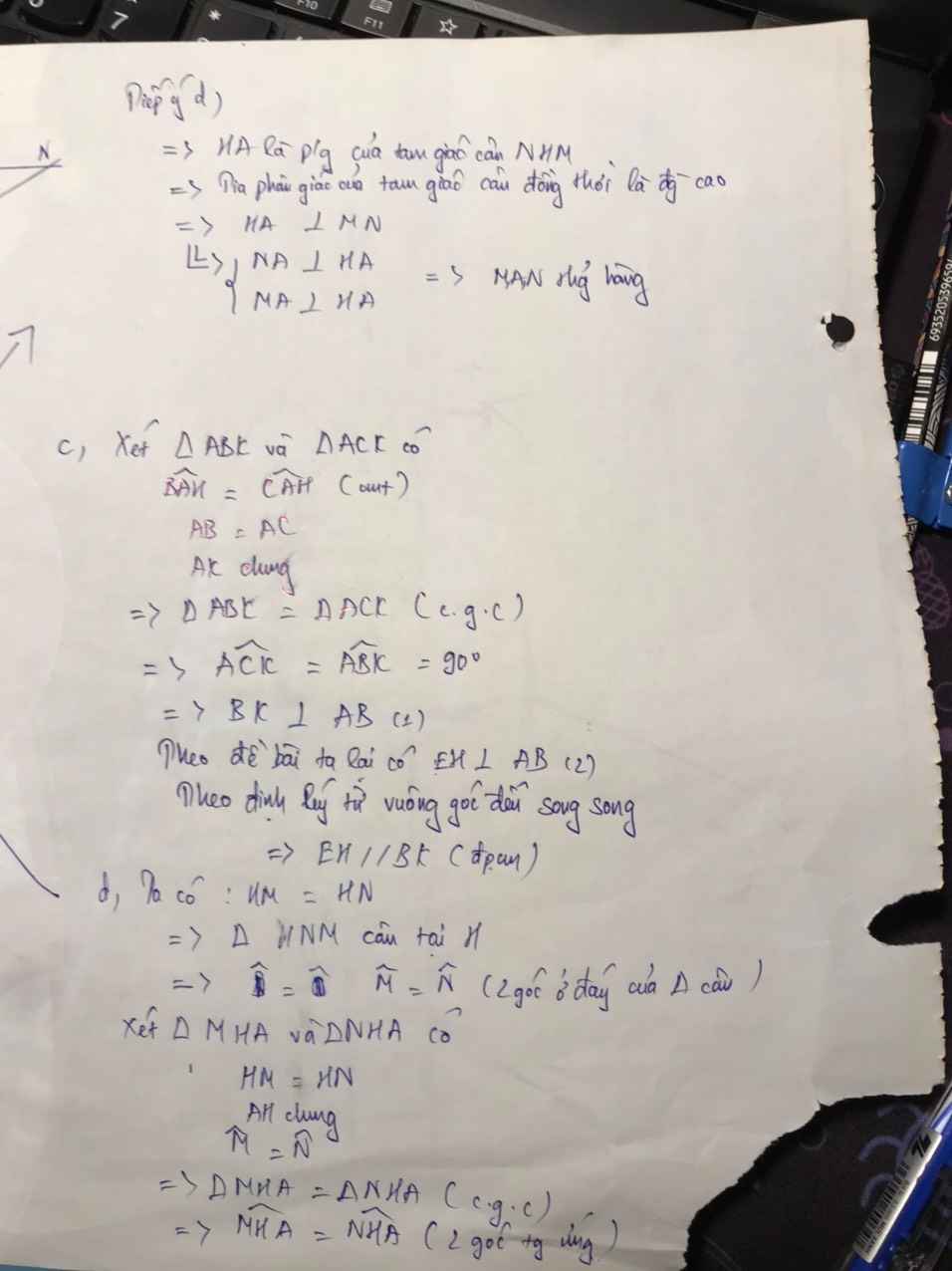Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác BAH
Có B+BAH=900(vì tam giác BAH vuông tại H)
500+BAH=900
=>BAH=900-500
=>BAH=400
Xét tam giác HAC
Có C+HAC=900(Tam giác HAC vuông tại H)
400+HAC= 900
HAC=900-400
HAC=500
B)Xét tam giác ABH
Có AB2 = HB2+AH2(Theo định lý Pi-ta-go)
AB2=32+42
AB2=25=52
AB=5
Xét tam giác CAH
Có AC2=AH2+HC2 (Theo định lý Pi-ta-go)
AC2=42+42=32=

a ) Do \(AH\perp BC\Rightarrow\)AH là đường cao của \(\Delta ABC\) cân tại A .Hay AH cũng là đường trung tuyến của \(\Delta ABC\) cân tại A .
\(\Rightarrow BH=HC\)
Xét \(\Delta BMH\) và \(\Delta CNH\) có : \(\widehat{BMH}=\widehat{CNH}=90^0\left(gt\right);BH=HC\left(cmt\right);\widehat{B}=\widehat{C}\left(gt\right)\)
\(\Rightarrow\) \(\Delta BMH\) = \(\Delta CNH\) (CH - GN) => BM = CN
Kết hợp với AB = AC => AM = AN hay \(\Delta AMN\) Cân tại A
b) \(\Delta AMN\) Cân tại A (cmt) \(\Rightarrow\widehat{BAC}=\frac{180^0-\widehat{AMN}}{2}\)(1)
\(\Delta ABC\) Cân tại A (gt) \(\Rightarrow\widehat{BAC}=\frac{180^0-\widehat{ABC}}{2}\)(2)
Từ (1);(2) \(\Rightarrow\widehat{AMN}=\widehat{ABC}\) Lại ở vị trí trong cùng phía \(\Rightarrow MN\\ \)BC
c) Áp dụng định lý Pytagore và 2 tam giác vuông\(BMH\) Và \(ANH\) ta có :
\(AH^2=AN^2+HN^2\)
\(BH^2=BM^2+MH^2\Rightarrow BM^2=BH^2-MH^2\)
\(\Rightarrow AH^2+BM^2=AN^2+HN^2+BH^2-MH^2=\left(AN^2+BH^2\right)+\left(HN^2-MH^2\right)\)
\(=AN^2+BH^2\)(đpcm)
Tam giác(TG) ABC cân tại A có đường cao AH => AH đồng thời là trung tuyến => BH=HC
TG ABC cân => Góc ABC = góc ACB (2goc đáy)
TG MBH = TG NCH (cạnh huyền-góc nhọn) => MB = NC (2ctu)
mà AB = AC (vì TG ABC cân) và AM + BM = AB , AN + NC = AC
=> AM = AN
=> TG AMN cân
b) AM = BM (CMT) và AN = NC (CMT) => MN là ddg TB của TG=> MN//BC

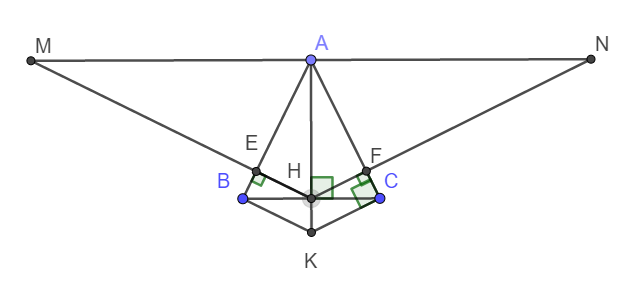
a) Xét tam giác vuông ABH và tam giác vuông ACH có:
Cạnh AH chung
AB = AC (gt)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (Hai góc tương ứng)
Vậy nên AH là tia phân giác góc BAC.
b) Xét hai tam giác vuông AEH và AFH có:
Cạnh AH chung
\(\widehat{EAH}=\widehat{FAH}\)
\(\Rightarrow\Delta AEH=\Delta AFH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HE=HF\) (Hai cạnh tương ứng)
Suy ra tam giác HEF cân tại E.
c) Dễ thấy \(\Delta ABK=\Delta ACK\left(c-g-c\right)\)
\(\Rightarrow\widehat{AKB}=\widehat{AKC}\)
Lại có \(\widehat{AKC}=\widehat{AHF}\) (Đồng vị)
\(\widehat{AHF}=\widehat{AHE}\) (Do \(\Delta AEH=\Delta AFH\) )
\(\Rightarrow\widehat{AKB}=\widehat{AHE}\) hay HE // BK
d) Ta có \(\Delta AHN=\Delta AHM\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAH}=\widehat{NAH}=90^o\)
\(\Rightarrow\widehat{MAN}=180^o\) hay M, N, A thẳng hàng.