Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình bạn tự vẽ nha
a)Vì tam giác ABC cân tại A
=> góc ABC=góc ACB
Xét tam giác ABH và tam giác ACH có
góc AHB= góc AHC(= 90 độ)
AB=AC(gỉa thiết)
góc ABC= góc ACB(chứng minh trên)
=> tam giác ABH = tam giác ACH(c/h-g/n) hoặc chứng minh theo trường hợp c/h-cgv cũng được
b)Xét tam giác ACH và tam giác DCH có
AH=DH(giả thiết)
góc AHC= góc DHC(= 90 độ)
cạnh HC chung
=>tam giác ACH = tam giác DCH(c.g.c)
=> AC=DC(2 cạnh tương ứng)

a) Xét hai tam giác vuông ABH và ACH ta có
AB = AC (gt)
\(\widehat{ABC}=\widehat{ACB}\)(gt)
Do đó: \(\Delta ABH=\Delta ACH\left(ch-gn\right)\)
b) Xét hai tam giác vuông AHB và DHC ta có
HA = HD (gt)
\(\widehat{AHB}=\widehat{CHD}\left(đđ\right)\)
Do đó: \(\Delta AHB=\Delta DHC\left(ch-gn\right)\)
=> AB = DC (căp cạnh tương ứng)
Mà AB = AC (gt) nên AC = DC
c) Ta có: \(\Delta AHB=\Delta DHC\)(câu a)
=> \(\widehat{BAG}=\widehat{GAC}\)(căp góc tương ứng)
Xét hai tam giác ABG và ACG ta có
AB = AC (gt)
\(\widehat{BAG}=\widehat{GAC}\left(cmt\right)\)
AG là cạnh chung
Do đó: \(\Delta ABG=\Delta ACG\left(c-g-c\right)\)
AE = AF (cặp cạnh tương ứng)
Ta có AE = \(\frac{1}{2}\)AB mà AB = AE và AE = AF
nên AF = \(\frac{1}{2}\)AC hay đường thẳng BG đi qua trung điểm F của AC
tk mk nhoa!!! ~3~

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
b) Xét ΔABH vuông tại H và ΔDCH vuông tại H có
BH=CH(ΔABH=ΔACH)
AH=DH(cmt)
Do đó: ΔABH=ΔDCH(hai cạnh góc vuông)
Suy ra: AB=DC(hai cạnh tương ứng)
mà AB=AC(ΔABC cân tại A)
nên DC=AC(Đpcm)

A B C H D E G F
a) Xét \(\Delta\)AHB vuông tại H và \(\Delta\)AHC vuông tại H có:
AH là cạnh chung
AB = AC (Vì \(\Delta\)ABC cân)
\(\Rightarrow\) \(\Delta\)AHB = \(\Delta\)AHC (ch + 1cgv)
b) Xét \(\Delta\)DHC vuông tại H và \(\Delta\)AHC vuông tại H, có:
CH là cạnh chung
HD = HA (gt)
\(\Rightarrow\) \(\Delta\)DHC = \(\Delta\)AHC (2cgv)
\(\Rightarrow\) DC = AC (2 cạnh tương ứng)
Nguyễn Ngô Minh Trí
hình và phần a bạn tham khảo của Kien Nguyen
b) Vì AH = HD (gt) mà H \(\in\) AD (gt)
=> H trung điểm AD (ĐN trung điểm)
=> CH là trung tuyến \(\Delta\)CAH (ĐN trung tuyến)
lại có: AH \(\perp\) BC (gt) hay AD \(\perp\) CH (D \(\in\) AH, H \(\in\) BC)
=> \(\Delta\)ACD cân tại C (dhnb)
=> AC = CD (ĐN \(\Delta\) cân)
c) Vì AH là đường cao của \(\Delta\)ABC (gt)
mà \(\Delta\)ABC cân tại A (gt)
=> AH là trung tuyến \(\Delta\)ABC (t/c \(\Delta\) cân)
Ta có: E trung điểm AB (gt)
=> CE là trung tuyến \(\Delta\)ABC (ĐN trung tuyến)
Xét \(\Delta\)ABC có: AH là trung tuyến BC (cmt)
CE là trung tuyến AB (cmt)
AH giao CE tại G (gt)
=> G là trọng tâm \(\Delta\)ABC (t/c 3 đường trung tuyến \(\Delta\))
=> BG là trung tuyến \(\Delta\)ABC (ĐN trọng tâm)
mà F là trung điểm AC (gt)
=> BG đi qua trung điểm F của AC

a, xét 2 t.giác vuông ABH và MBH có:
AH=MH(gt)
HB cạnh chung
=> t.giác ABH=t.giác MBH(cạnh góc vuông-cạnh góc vuông)
b, vì I là trung điểm của BC nên AI=1/2 BC<=> AI=IC
=>t.giác AIC cân tại I
xét 2 t.giác vuông ABC và CDA có:
AC cạnh chung
\(\widehat{ACB}\)=\(\widehat{CAD}\)(t.giác AIC cân tại I)
=>t.giác ABC=t.giác CDA(cạnh góc vuông-góc nhọn)
=> CD=AB(2 cạnh tương ứng)
c,dễ nên tự làm
a, xét 2 t.giác vuông ABH và MBH có:
AH=MH(gt)
HB cạnh chung
=> t.giác ABH=t.giác MBH(cạnh góc vuông-cạnh góc vuông)
b, vì I là trung điểm của BC nên AI=1/2 BC<=> AI=IC
=>t.giác AIC cân tại I
xét 2 t.giác vuông ABC và CDA có:
AC cạnh chung
góc ACB = góc CAD (t.giác AIC cân tại I)
=>t.giác ABC=t.giác CDA(cạnh góc vuông-góc nhọn)
=> CD=AB(2 cạnh tương ứng)
c) Ta có \(\hept{\begin{cases}\widehat{ACB+\widehat{ABC=90}độ}\\HBM+HMB=90\end{cases}}\)(do tam giác ABC zuông tại a , do tam giác BHM zuông tại H
mà ABH=HBM do ( Tam giác AHB=tam giác HBM cmt)
=> ACB=HMB hay ACB =AMB
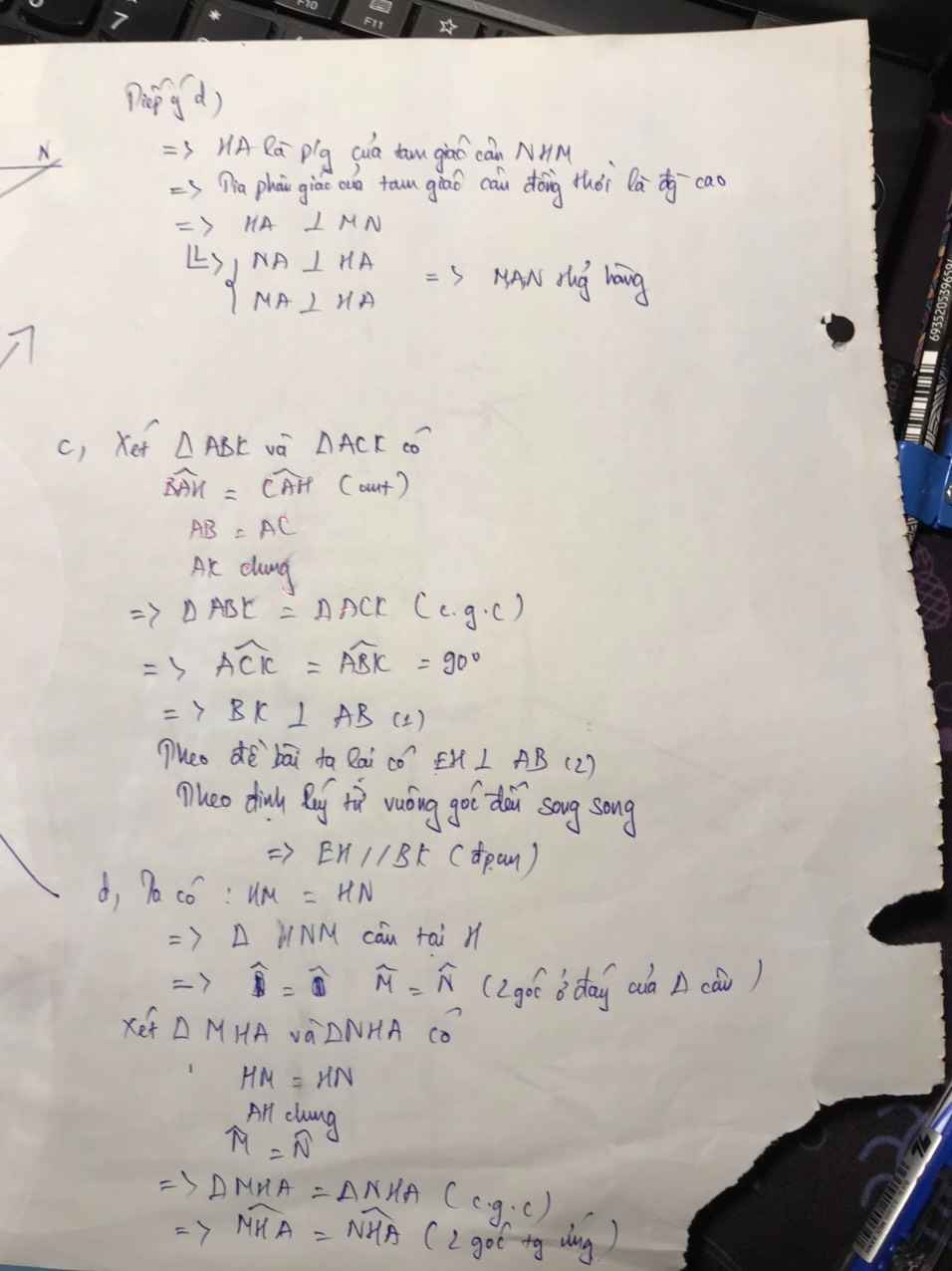




Mashiro ShiinaPhạm Nguyễn Tất ĐạtNhã DoanhtthNeetKien NguyenNguyễn Thanh HằngĐời về cơ bản là buồn... cười!!!Trần Đăng NhấtMến VũNguyễn Huy TúNguyễn Huy ThắngAkai Harumasoyeon_Tiểubàng giảiPhương AnVõ Đông Anh Tuấn