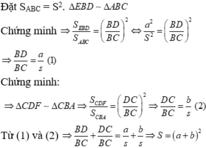Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
ta có G là trọng tâm của tam giác ABC.
\(\hept{\begin{cases}\Rightarrow BH=GH=GD\\\Rightarrow EG=GK=KC\end{cases}}\)
hay G là trung điểm của EK và HD.
tứ giác EDKH có 2 đường chéo cắt nhau tại trung điểm mỗi đường
do đó tứ giác EDKH là hình bình hành.
b) để hình bình hành EDKH là hình chữ nhật thì EK=HD
⇒BD=EC⇒ΔABCcân
vậy để hình bình hành EDKH là hình chữ nhật thì tam giác ABC cân
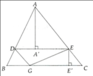
c) vẽ đường cao AI vuông góc với BC.
khi đó AI cũng là đường trung tuyến.
\(\Rightarrow AG=\frac{2}{3}AI\)
ta có :\(\hept{\begin{cases}BE=AE\\AD=DC\end{cases}}\) nên ED là đường trung bình của tam giác ABC.
⇒\(\hept{\begin{cases}ED//BC\\2ED=BC\end{cases}}\)
vì ED//BC và AI⊥BC nên ED⊥AI
đồng thời EH⊥ED nên EH//AI.
ta có: \(\hept{\begin{cases}EH//AI\\BE=EA\end{cases}}\)\(\Rightarrow AH=\frac{AG}{2}\)
hay \(EH=\frac{\frac{2}{3}AI}{2}=\frac{1}{3}AI\Leftrightarrow3EH=AI\)
\(S\Delta ABC=\frac{AI.BC}{2}=\frac{3EH.2ED}{2}=3EH.ED\)=\(3S_{EDHK}\)
vậy\(\frac{S_{EDHK}}{S_{\Delta ABC}}=\frac{1}{3}\)
CHÚC BẠN HỌC TỐT