Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng số đo các góc của hình tam giác luôn bằng 360 độ
Số đo của góc A là:360:(3+5+7)x3=72 độ
Số đo của góc B là:72:3x5=120 độ
Số đo của góc C là:360-120-72=168 độ

Goi 3 acnh lan luot la a;b;c
số đo các cạnh tỉ lệ với 2,3,4.
Vì tổng 3 góc của 1 tam giác =180
=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{180}{9}=20\)
=> a= 20.2=40
b= 20.3=60
c= 20.4=80

1:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: a=40; b=60; c=80
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\)
nen BC<AC<AB
2: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{b}{\dfrac{1}{3}}=\dfrac{c}{\dfrac{1}{4}}=\dfrac{b+c}{\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{70}{\dfrac{7}{12}}=120\)
Do đó: b=40; c=30
Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB

Gọi số đo của 3 góc tam giác abc là x,y,z (x,y,z \(\ne\)0 )
Vì x,y,z lần lượt tỉ lệ với 1,3,5 nên x,y,z lần lượt là \(\frac{x}{1},\frac{y}{3},\frac{z}{5}\)
Vì tổng tam giác abc = 180o (định lí) nên x + y + z = 180
Áp dụng tính chất dãy tỉ số bằng nhau, ta có\(\frac{x}{1}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{1+3+5}=\frac{180^o}{9}=20^o\)
Do đó, x = 20 . 1 = 20
y = 20 . 3 = 60
z = 20 . 5 = 100
Vậy số đo mỗi góc tam giác abc lần lượt là 20,60,100

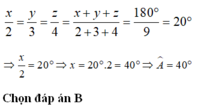
Gọi số góc `A,B,C` lần lượt là `a,b,c`
Theo đề ra ta có : `a/2=b/3=c/4` và `a+b+c=180`
ADTC dãy tỉ số bằng nhau ta có :
`a/2=b/3=c/4 =(a+b+c)/(2+3+4)=180/9= 20`
`=> a/2=20=>a=20.2=40`
Vậy số đo góc A là `40`
a