Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

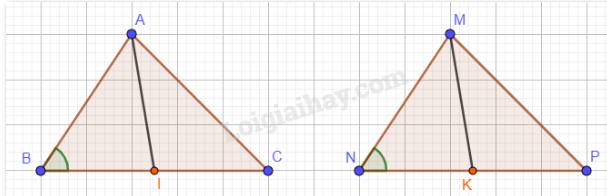
Hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM nên \(\Delta ABC = \Delta MNP\)(c.c.c)
Suy ra: \(\widehat {ABI} = \widehat {MNK}\) ( 2 góc tương ứng).
Ta có: I, K lần lượt là trung điểm của BC và NP mà BC = NP, suy ra: \(BI = NK\).
Xét tam giác ABI và tam giác MNK có:
AB = MN;
\(\widehat {ABI} = \widehat {MNK}\);
BI = NK.
Vậy \(\Delta ABI = \Delta MNK\)(c.g.c). Suy ra: AI = MK (2 cạnh tương ứng).
Vậy AI = MK.

a) Xét △MIQ và △NIP ta có:
IM=IN (gt)
∠MIQ=∠NIP(2 góc đối đỉnh)
MQ=MP (gt)
Vậy : △MIQ = △NIP (c.g.c)
Vậy: QM = NP (2 cạnh tương ứng)
⇒ ∠MQI = ∠IPN (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong
Vậy : QM // NP
b) Xét △MEK và △PEN ta có:
EM = EP (gt)
∠MEK =∠PEN (2 góc đối đỉnh)
EK = EN (gt)
⇒ △MEK = △PEN (c.g.c)
⇒ ∠EMK = ∠EPN (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong
Vậy: MK//PN
c) Từ câu a và câu b, ta có : QM//NP và MK//PN
Vậy M,Q,K thẳng hàng.(1)
Ta có:△MEK=△PEN (theo câu b)
⇒ MK=NP (2 cạnh tương ứng)
⇒ QM=NP (theo câu a) và MK=NP(chứng minh trên)⇒QM=MK (2)
Từ (1) và (2), suy ra: M là trung điểm của đoạn thẳng QK.
Mình ko biết là A trog câu c) ở đâu nên mình đổi thành Q nha!

B ở đâu vậy bạn ? Trong đề làm gì có nói kẻ B mà từ B đã kẻ đường vuông góc rồi ?