Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chẳng hiểu gì.Hỏi cô Thủy hoặc thầy Phong hoặc thầy Huy.Không thì vào goodgle.

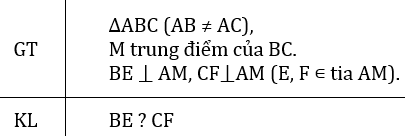
Hai tam giác vuông BME, CMF có:
BM=MC(gt)
ˆBMEBME^=ˆCMFCMF^(đối đỉnh)
Nên ∆BME=∆CMF(cạnh huyền- góc nhọn).
Suy ra BE=CF.

Lời giải:
Hai tam giác vuông BME và CMF có
⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)
⇒ BE = CF (hai cạnh tương ứng).
Kiến thức áp dụng
+ Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
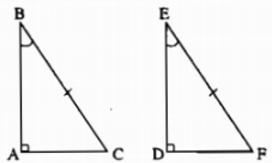
ΔABC vuông tại A và ΔDEF vuông tại D có:
BC = EF
∠B = ∠E
⇒ΔABC = ΔDEF

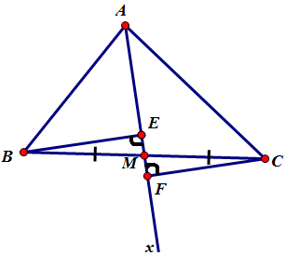
Ta có hình vẽ:
x A B C M E F
Δ CFM có: CFM + FMC + MCF = 180o
Δ EMB có: EMB + MBE + BEM = 180o
Mà CFM = MEB = 90o
FMC = BME (đối đỉnh) nên MCF = MBE
Xét Δ MCF và Δ MBE có:
MCF = MBE (cmt)
CM = BM (gt)
FMC = EMB (đối đỉnh)
Do đó, Δ MCF = Δ MBE (c.g.c)
=> CF = BE (2 cạnh tương ứng)

Ta có hình vẽ trên:
Xét 2 tam giác vuông MBE và tam giác MCF có:
BM = MC (gt)
góc M1 = góc M2 (đối đỉnh)
suy ra tam giác MBE = tam giác MCF (cạnh huyền - góc nhọn)
suy ra BE = CF (2 cạnh tương ứng)
Vậy BE = CF

a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)
Do đó: ΔBME=ΔCMF
Suy ra: BE=CF

A B M C x E F
a) Xét \(\Delta\)BME & \(\Delta\)CMF có:
góc BEM= góc CFM= 90 độ
BM=CM( vì M là trung điểm của BC)
góc EMB= góc FMC(2 góc đối đỉnh)
=>\(\Delta\)BME=\(\Delta\)CMF(g.c.g)
b)Theo a) \(\Delta\)BME=\(\Delta\)CMF
=> ME=MF(2 cạnh tương ứng)
c) Xét \(\Delta\)CME & \(\Delta\)BMF có:
ME=MF( theo c/m b)
góc CME= góc BMF(2 góc đối đỉnh)
BM=CM( vì M là trung điểm BC)
=>\(\Delta\)CME=\(\Delta\)BMF(c.g.c)
=>CE=BF(2 cạnh tương ứng)
d)Theo c) \(\Delta\)CME=\(\Delta\)BMF
=>góc ECM= góc FBM(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong=>CE//BF
e) Ta có: \(\Delta\)BME=\(\Delta\)CMF( theo c/m a)
=> góc BEM= góc CFM(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong=>BE//CF

Giải thích các bước giải:
BE ⊥ AM, CF⊥AM
=> BE // CF
a) Xét Δ vuông BME và Δ vuông CMF có:
BM = MC ( M là tđ BC )
B1 = C1 ( so le trong )
=> Δ ... = Δ ... ( ch - gn)
b) ME = MF ( cạnh tương ứng )
c) Xét Δ MEC và Δ MFB có:
M1 = M2 (đối đỉnh)
ME = MF (cmt)
BM = CM (cmt)
=> Δ ... = Δ ... ( cgc )
=> CE = BF
d)
Ta có: C2 = B2 (Δ MEC = Δ MFB)
Mà 2 góc này ở vị trí so le trong
=> CE // BF
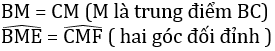
Kí hiệu tam giác là t/g nhé
a) Có: BE _|_ Ax (gt)
CF _|_ Ax (gt)
Suy ra BE // CF (1)
Xét t/g EMB vuông tại E và t/g FMC vuông tại F có:
BM = CM (gt)
EMB = FMC ( đối đỉnh)
Do đó, t/g EMB = t/g FMC ( cạnh huyền và góc nhọn kề)
=> BE = CF (2 cạnh tương ứng) (2)
ME = MF (2 cạnh tương ứng) (3)
(1); (2) và (3) là đpcm
b) Xét t/g EMC và t/g FMB có:
EM = MF (câu a)
EMC = FMB ( đối đỉnh)
CM = BM (gt)
Do đó, t/g EMC = t/g FMB (c.g.c)
=> CE = BF (2 cạnh tương ứng) (4)
ECM = FBM (2 góc tương ứng)
Mà ECM và FBM là 2 góc so le trong
Nên EC // BF (5)
(4) và (5) là đpcm