Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

Bạn tự vẽ hình nha
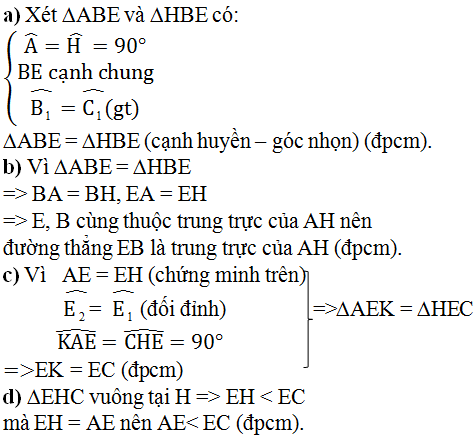
a) CM: tam giác ABE = tam giác HBE
Xét tam giác ABE (Â=90o) và tam giác HBE (góc H= 90o), ta có:
Góc ABE = Góc HBE ( BE là p/g góc B)
BE là cạnh chung
Vậy: tam giác ABE = tam giác HBE ( cạnh huyền-góc nhọn)
c) CM: NM=NC
Xét tam giác AEM và tam giác HEC, ta có:
góc AEM = góc HEC ( đối đỉnh)
AE = HE (tam giác ABE = tam gác HBE)
góc EAM = góc EHC = 90o
Vậy: tam giác AEM = tam giác HEC (g-c-g)
Ta có: AB+AM=BM
BH+HC=BC
mà BA=BH(tam giác BAE= tam giác BEH)
AM=HC(tam giác AEM= tam giác HEC)
nên BM=BC
Xét tam giác NBM và tam giác NBC, ta có:
NB là cạnh chung
góc NBM= góc NBC ( BE là p/g góc B)
BM=BC (cmt)
Vậy tam giác NBM= tam giác NBC ( c-g-c)
=> NM=NC ( 2 cạnh tương ứng)
Sorry vì mình khong làm được bài b

Trả lời................
Tớ không biết đúng hay sai đâu nha Ý Phạm
a,Xét tam giác ABE (BAE^ vuông) và tam giác HBE (BHE^ vuông) có:
BE=BE (cạnh chung)
ABE^=HBE^
⟹ ABE^=HBE^(ch+gn)
b,Ta có:
BA=BH (tam giác ABE = tam giác HBE)
EA=EH (________________________)
⟹ BE là đường trung trực của AH
c,Xét tam giác EKA và tam giác ECH có
AE=EH (gt)
EAK^=EHK^(=90o)
AEK^=HEC^(đối đỉnh)
⟹Tam giác EKA=tam giacsEHK (g-c-g)
⟹EK=EH ( cạnh tương ứng)
d,Từ điểm E đến đường thẳng HC có:
EH là đường vuông góc
EC là đường xiên
⟹EH<EC( quan hệ đường vuông góc)
Mà EH=AE(tam giác ABE = tam giác HBE)
⟹AE<AC

giúp mình với nhé mai mình thi cuối học kì I môn toán rồi. Chúc các bạn có một kì thi tốt đẹp.
đề bài sai à
câu a tam giác vuông tại A mà góc B = 90o suy ra góc C = 0o à
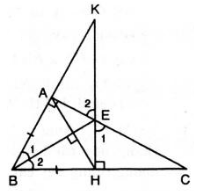


Ta có hình vẽ: B A C K F E H 1 2 1 2 1 2 1 2 I
a) Xét 2 \(\Delta\)vuông \(ABE\)và \(\Delta HBE\) có:
góc B1 = góc B2 (gt)
BE là cạnh huyền chung
=> \(\Delta ABE\) = \(\Delta HBE\) (cạnh huyền - góc nhọn)
b) Xét 2 \(\Delta\) \(ABI\)và \(\Delta HBI\) có:
góc B1 = góc B2 (gt)
AB = HB (vì \(\Delta ABE\) = \(\Delta HBE\))
AI là cạnh chung
=> \(\Delta ABI\)= \(\Delta HBI\) (c-g-c)
=> AI = HI (2 cạnh tương ứng)
=> góc I1 = góc I2 (2 góc tương ứng)
mà góc I1 + góc I2 = 180 độ
=> góc I1 = góc I2 = 180/2= 90 độ
=> BI \(\perp\) AH
=> BI là đường trung trực của đoạn thẳng AH
=> BE cũng là đường trung trực của đoạn thẳng AH (đpcm) (vì B, I , E nằm trên cùng 1 đoạn thẳng)
c)Xét \(\Delta\) vuông HEC có:
EC là cạnh đối diên với góc vuông (góc EHC)
=> EC là cạnh lớn nhất
=> EC > HE
mặt \(\ne\) HE = AE (vì\(\Delta ABE\) = \(\Delta HBE\))
=> EC > AE
d) Xét \(\Delta BKC\) có:
KH là đường cao thứ 1
CA là đường cao thứ 2
=> BF là đường cao thứ 3
=> BF \(\perp\) KC
=> BE \(\perp\) KC (đpcm) (vì B, E , F nằm trên cùng 1 đoạn thẳng)