
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

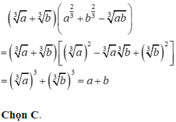

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

Câu a, b thì Nguyễn Quang Duy làm đúng rồi.
c) \(a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\)
d) \(\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}\)

a)
\(A=\dfrac{a^{\dfrac{4}{3}}\left(a^{-\dfrac{1}{3}}+a^{\dfrac{2}{3}}\right)}{a^{\dfrac{1}{4}}\left(a^{\dfrac{3}{4}}+a^{-\dfrac{1}{4}}\right)}=\dfrac{a^{\left(\dfrac{4}{3}-\dfrac{1}{3}\right)+}a^{\left(\dfrac{4}{3}+\dfrac{2}{3}\right)}}{a^{\left(\dfrac{1}{4}+\dfrac{3}{4}\right)}+a^{\left(\dfrac{1}{4}-\dfrac{1}{4}\right)}}=\dfrac{a+a^2}{a+1}=\dfrac{a\left(a+1\right)}{a+1}\)
\(a>0\Rightarrow a+1\ne0\) \(\Rightarrow A=a\)

a) \(A=\left[\left(\frac{1}{5}\right)^2\right]^{\frac{-3}{2}}-\left[2^{-3}\right]^{\frac{-2}{3}}=5^3-2^2=121\)
b) \(B=6^2+\left[\left(\frac{1}{5}\right)^{\frac{3}{4}}\right]^{-4}=6^2+5^3=161\)
c) \(C=\frac{a^{\sqrt{5}+3}.a^{\sqrt{5}\left(\sqrt{5}-1\right)}}{\left(a^{2\sqrt{2}-1}\right)^{2\sqrt{2}+1}}=\frac{a^{\sqrt{5}+3}.a^{5-\sqrt{5}}}{a^{\left(2\sqrt{2}\right)^2-1^2}}\)
\(=\frac{a^{\sqrt{5}+3+5-\sqrt{5}}}{a^{8-1}}=\frac{a^8}{a^7}=a\)
d) \(D=\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)^2:\left(b-2b\sqrt{\frac{b}{a}}+\frac{b^2}{a}\right)\)
\(=\left(\sqrt{a}-\sqrt{b}\right)^2:b\left[1-2\sqrt{\frac{b}{a}}+\left(\sqrt{\frac{b}{a}}\right)^2\right]\)
\(=\left(\sqrt{a}-\sqrt{b}\right)^2:b\left(1-\sqrt{b}a\right)^2\)

a) \(A=\frac{a^{\frac{5}{2}}\left(a^{\frac{1}{2}}-a^{\frac{-3}{2}}\right)}{a^{\frac{1}{2}}\left(a^{\frac{-1}{2}}-a^{\frac{3}{2}}\right)}=\frac{a^3-a}{1-a^2}=-a\)
Do đó : \(A=-\left(\pi-3\sqrt{2}\right)=3\sqrt{2}-\pi\)
b) Rút gọn B ta có :
\(B=\left(a^{\frac{1}{3}}+b^{\frac{1}{3}}\right)\left[\left(a^{\frac{1}{3}}\right)^2+\left(b^{\frac{1}{3}}\right)^2\right]=\left(a^{\frac{1}{3}}\right)^3+\left(b^{\frac{1}{3}}\right)^3=a+b\)
Do đó :
\(B=\left(7-\sqrt{2}\right)+\left(\sqrt{2}+3\right)=10\)

\(I=\frac{a^{\frac{4}{3}}-8a^{\frac{2}{3}}b}{a^{\frac{2}{3}}+2\sqrt[3]{ab}+4b^{\frac{2}{3}}}\left(1-2\sqrt[3]{\frac{b}{a}}\right)^{-1}-a^{\frac{2}{3}}=\frac{a^{\frac{1}{3}}\left(a-8b\right)}{a^{\frac{2}{3}}+2a^{\frac{1}{3}}.b^{\frac{1}{3}}+4b^{\frac{2}{3}}}\left(\frac{\sqrt[3]{a}-2\sqrt[3]{b}}{\sqrt[3]{a}}\right)^{-1}-a^{\frac{2}{3}}\)
\(=\frac{\sqrt[3]{a}\left[\left(\sqrt[3]{a}\right)^3-\left(2\sqrt[3]{b}\right)^3\right]}{a^{\frac{2}{3}}+2\sqrt[3]{ab}+4b^{\frac{2}{3}}}.\frac{\sqrt[3]{a}}{\sqrt[3]{a}-2\sqrt[3]{b}}-a^{\frac{2}{3}}\)
\(=\frac{\left(\sqrt[3]{a}\right)^2\left(\sqrt[3]{a}-2\sqrt[3]{b}\right)\left[\left(\sqrt[3]{a}\right)^2+2\sqrt[3]{ab}+\left(2\sqrt[3]{b}\right)^2\right]}{\left(\sqrt[3]{a}-a\sqrt[3]{b}\right)\left[\left(\sqrt[3]{a}\right)^2+2\sqrt[3]{ab}+\left(2\sqrt[3]{b}\right)^2\right]}-a^{\frac{2}{3}}=a^{\frac{2}{3}}-a^{\frac{2}{3}}=0\)

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\((a^2+b^2+1)(1+1+c^2)\geq (a+b+c)^2\)
\(\Leftrightarrow a^2+b^2+1\geq \frac{(a+b+c)^2}{c^2+2}\Rightarrow \frac{1}{a^2+b^2+1}\leq \frac{c^2+2}{(a+b+c)^2}\)
Thiết lập tương tự với các phân thức còn lại và cộng theo vế:
\(\Rightarrow A=\frac{1}{a^2+b^2+1}+\frac{1}{b^2+c^2+1}+\frac{1}{c^2+a^2+1}\leq \frac{6+a^2+b^2+c^2}{(a+b+c)^2}\)
\(\Leftrightarrow A\leq \frac{2(ab+bc+ac)+a^2+b^2+c^2}{(a+b+c)^2}=\frac{(a+b+c)^2}{(a+b+c)^2}=1\)
Vậy \((\frac{1}{a^2+b^2+1}+\frac{1}{b^2+c^2+1}+\frac{1}{c^2+a^2+1})_{\max}=1\Leftrightarrow a=b=c=1\)
Cho 2 tập hợp A và B. Biết tập hợp B khác rỗng, số phần tử của tập B gấp đôi số phần tử của tập A∩B và A∪B có 10 phần tử. Hỏi tập A và B có bao nhiêu phần tử? Hãy xét các trường hợp xảy ra và dùng biểu đồ Ven minh họa?

Bài 3:
Áp dụng các hằng đẳng thức đáng nhớ ta có:
$C=a^4+b^4=(a^2+b^2)^2-2a^2b^2$
$=[(a+b)^2-2ab]^2-2(ab)^2$
$=(8^2-2.15)^2-2.15^2=706$
Bài 2:
a)
$D=-x^2+6x-11=-11-(x^2-6x)=-2-(x^2-6x+9)$
$=-2-(x-3)^2$
Vì $(x-3)^2\geq 0$ với mọi $x$ nên $D=-2-(x-3)^2\leq -2$
Vậy GTLN của $D$ là $-2$ khi $(x-3)^2=0\Leftrightarrow x=3$
b)
$F=4x-x^2+1=1-(x^2-4x)=5-(x^2-4x+4)=5-(x-2)^2$
$\leq 5-0=5$
Vậy $F_{\max}=5$. Giá trị này được khi $(x-2)^2=0\leftrightarrow x=2$