Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
7/ Em sửa lại đề ạ
Cho hai số thực dương a, b thỏa mãn a+b=4ab
Chứng minh rằng \(\frac{a}{4b^2+1}+\frac{b}{4a^2+1}\ge\frac{1}{2}\)
Đổi biến \(\left(a,b\right)\rightarrow\left(\frac{1}{x},\frac{1}{y}\right)\)
Từ giả thiết => x+y=4
Ta có: BĐT cần CM tương đương với:
\(\frac{\frac{1}{x}}{\frac{4}{y^2}+1}+\frac{\frac{1}{y}}{\frac{4}{x^2}+1}\ge\frac{1}{2}\)\(\Leftrightarrow\frac{y^2}{x\left(4+y^2\right)}+\frac{x^2}{y\left(4+x^2\right)}\ge\frac{1}{2}\left(1\right)\)
Áp dụng BĐT Schwarz, ta có:
∑\(\frac{x^2}{y\left(4+x^2\right)}\ge\frac{\left(x+y\right)^2}{4\left(x+y\right)+xy^2+x^2y}=\frac{16}{16+xy^2+x^2y}\)
Ta chỉ cần chứng minh:
\(xy^2+x^2y\le16\Leftrightarrow xy^2+x^2y\le\frac{1}{4}\left(x+y\right)^3\)
\(\Leftrightarrow xy^2+x^2y\le x^3+y^3\)(luôn đúng)
Do đó (1) đúng. BĐT được chứng minh. Dấu "=" xảy ra khi x=y=2⇔a=b=\(\frac{1}{2}\)
6. (chuyên Hòa Bình)
Cho các số dương x, y, z thỏa mãn: xy+zx+4yz=32
Tìm giá trị nhỏ nhất của\(P=x^2+16y^2+16z^2\)
Áp dụng bất đẳng thức Cauchy cho ba số dương x,y,z ta có
\(\hept{\begin{cases}8y^2+\frac{1}{2}x^2\ge2\sqrt{8y^2.\frac{1}{2}x^2}=4xy\\8z^2+\frac{1}{2}x^2\ge2\sqrt{8z^2.\frac{1}{2}x^2}=4xz\\8y^2+8z^2\ge2\sqrt{8y^2.8z^2}=16yz\end{cases}}\)
Cộng từng vế của ba bđt trên ta có
\(P\ge4\left(xy+xz+4yz\right)=4.32=128\)
Đáp án D.
Gọi M a ; b là điểm biểu diễn số phức z = a + b i . Đặt I = 1 ; 1 , A 7 ; 9 và B 0 ; 8
Ta xét bài toán: Tìm điểm M thuộc đường tròn C có tâm I, bán kính R = 5 sao cho biểu thức P = M A + 2 M B đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K x ; y sao cho M A = 2 M K ∀ M ∈ C .
Ta có
M A = 2 M K ⇔ M A 2 = 4 M K 2 ⇔ M I → + I A → 2 = 4 M I → + I K → 2
⇔ M I 2 + I A 2 + 2 M I → . I A → = 4 M I 2 + I K 2 + 2 M I → . I K →
⇔ 2 M I → I A → − 4 I K → = 3 R 2 + 4 I K 2 − I A 2 *
(*) luôn đúng ∀ M ∈ C ⇔ I A → − 4 I K → = 0 → 3 R 2 + 4 I K 2 − I A 2 = 0 .
I A → − 4 I K → = 0 → ⇔ 4 x − 1 = 6 4 y − 1 = 8 ⇔ x = 5 2 y = 3
Thử trực tiếp ta thấy K 5 2 ; 3 thỏa mãn 3 R 2 + 4 I K 2 − I A 2 = 0 .
Ta cos M A + 2 M B = 2 M K + 2 M B = 2 M K + M B ≥ 2 K B .
Vì B I 2 = 1 2 + 7 2 = 50 > R 2 = 25 nên B nằm ngoài (C).
Vì K I 2 = 3 2 2 + 2 2 < R 2 = 25 nên K nằm trong (C) .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK . Do đó M A + 2 M B nhỏ nhất khi và chỉ khi M là giao điểm của (C) và đường thẳng BK.
Phương trình đường thẳng B K : 2 x + y − 8 = 0 .
Phương trình đường tròn C : x − 1 2 + y − 1 2 = 25 .
Tọa độ điểm M là nghiệm của hệ
2 x + y = 8 x − 1 2 + y − 1 2 = 25 ⇔ x = 1 y = 6
hoặc x = 5 y = − 2 .
Thử lại thấy M 1 ; 6 thuộc đoạn BK.
Vậy a = 1, b = 6 ⇒ a + b = 7 .
Chọn đáp án B
Từ giả thiết ta có:
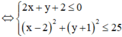
Suy ra tập hợp các điểm biểu diễn số phức z là miền mặt phẳng
(T) thỏa mãn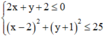 
(miền tô đậm trong hình vẽ bên
Gọi A, B là các giao điểm của đường thẳng 2 x + y + 2 = 0 và đường tròn (C’) : x - 2 2 + y + 1 2 = 25
Ta tìm được A(2; -6) và B(-2; 2)
Ta có :
Đường tròn (C) cắt miền (T) khi và chỉ khi
Theo hệ quả của bất đẳng thức Cauchy - Schwarz
\(\Rightarrow x^2+y^2+z^2\ge xy+yz+xz\)
Mà \(x^2+y^2+z^2\le3\)
\(\Rightarrow xy+yz+xz\le3\)
Ta có \(P=\dfrac{1}{1+xy}+\dfrac{1}{1+yz}+\dfrac{1}{1+xz}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow P\ge\dfrac{\left(1+1+1\right)^2}{xy+1+yz+1+xz+1}=\dfrac{9}{xy+yz+xz+3}\) (1)
Ta có \(xy+yz+xz\le3\)
\(\Rightarrow xy+yz+xz+3\le6\)
\(\Rightarrow\dfrac{9}{xy+yz+xz+3}\ge\dfrac{9}{6}=\dfrac{3}{2}\) (2)
Từ (1) và (2)
\(\Rightarrow P\ge\dfrac{3}{2}\)
Vậy \(P_{min}=\dfrac{3}{2}\)
Dấu " = " xảy ra khi \(x=y=z=1\)
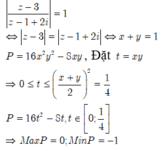
Chọn đáp án C