
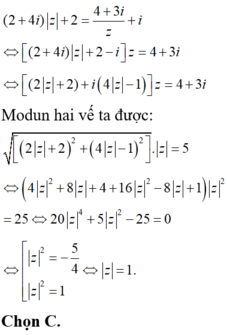
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

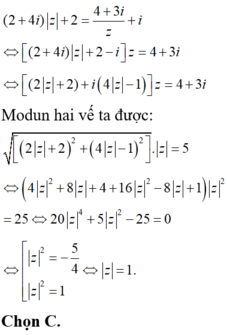

Đáp án A
Cho số phức z = x + yi (x,y ∈ R) , S(x,y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
![]()
![]()
Lấy các điểm A(2; - 3), B( - 2; - 1)
Phương trình
![]()
=> Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;
-
3), B(
-
2;
-
1) và có độ dài trục lớn là ![]()
Lấy M(4;
-
4). Dễ dàng kiểm tra được 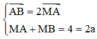
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB => I(0;
-
2), N là điểm đối xứng của M qua I. Khi đó, với mọi điểm ![]()
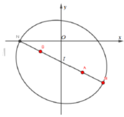
![]() khi và chỉ khi S trùng N
khi và chỉ khi S trùng N ![]() khi và chỉ khi
khi và chỉ khi ![]()

z + i - 1 = z - 2 i ⇔ a + 1 + b + 1 = a + b - 2 i
Với z = a + bi
a + 1 2 + b + 1 2 = a 2 + b - 2 2 ⇔ a + b = 1
Từ đây ta có z = a 2 + b 2 ≥ a + b 2 = 2 2
Đáp án cần chọn là A