Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta=m^2+8\ge8\forall m\)
=> \(\Delta>0\)=> PT có 2 nghiệm phân biệt với mọi m
Theo Vi-et ta có: \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-2\end{cases}}\)
\(x_1^2+x_2^2-3x_1x_2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-5x_1x_2=14\)
\(\Leftrightarrow m^2=14-10=4\)
\(\Leftrightarrow m=\pm2\)

Vi-ét\(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-2\end{cases}}\)
\(x_1^2+x_2^2-3x_1x_2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-5x_1x_2=14\)
\(\Leftrightarrow m^2=14-10\)
\(\Leftrightarrow m=\pm2\)

a, \(\Delta=\left(-m\right)^2-4\left(-2\right)=m^2+8>0\forall m\in R\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt \(\forall m\)
b, Theo vi-lét ta có: \(x_1+x_2=m\) và \(x_1x_2=-2\)
Ta có: \(x^2_1+x^2_2-3x_1x_2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-5x_1x_2=14\)
\(\Leftrightarrow m^2+10=14\)
\(\Leftrightarrow m^2=4\)
\(\Leftrightarrow m=\pm2\)
Vậy .............

Pt có nghiệm khi \(\Delta\ge0\)
\(\Leftrightarrow\left(m-1\right)^2-4\left(5m-5\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-20m+20\ge0\)
\(\Leftrightarrow m^2-22m+21\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}m\le1\\m\ge21\end{cases}}\)
Theo hệ thức Vi-ét \(\hept{\begin{cases}x_1+x_2=1-m\\x_1x_2=5m-5\end{cases}}\)
Chắc đề là \(x_1^2+x_2^2=3x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=5x_1x_2\)
\(\Leftrightarrow\left(1-m\right)^2=5.\left(5m-5\right)\)
\(\Leftrightarrow1-2m+m^2=25m-25\)
\(\Leftrightarrow m^2-27m+26=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=26\\m=1\end{cases}\left(Tm\right)}\)
Vậy .........

Phương trình có 2 nghiệm phân biệt khi:
\(\Delta'=1-\left(m-1\right)>0\Rightarrow m< 2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(m-1\right)=10\)
\(\Leftrightarrow m=-2\) (thỏa mãn)
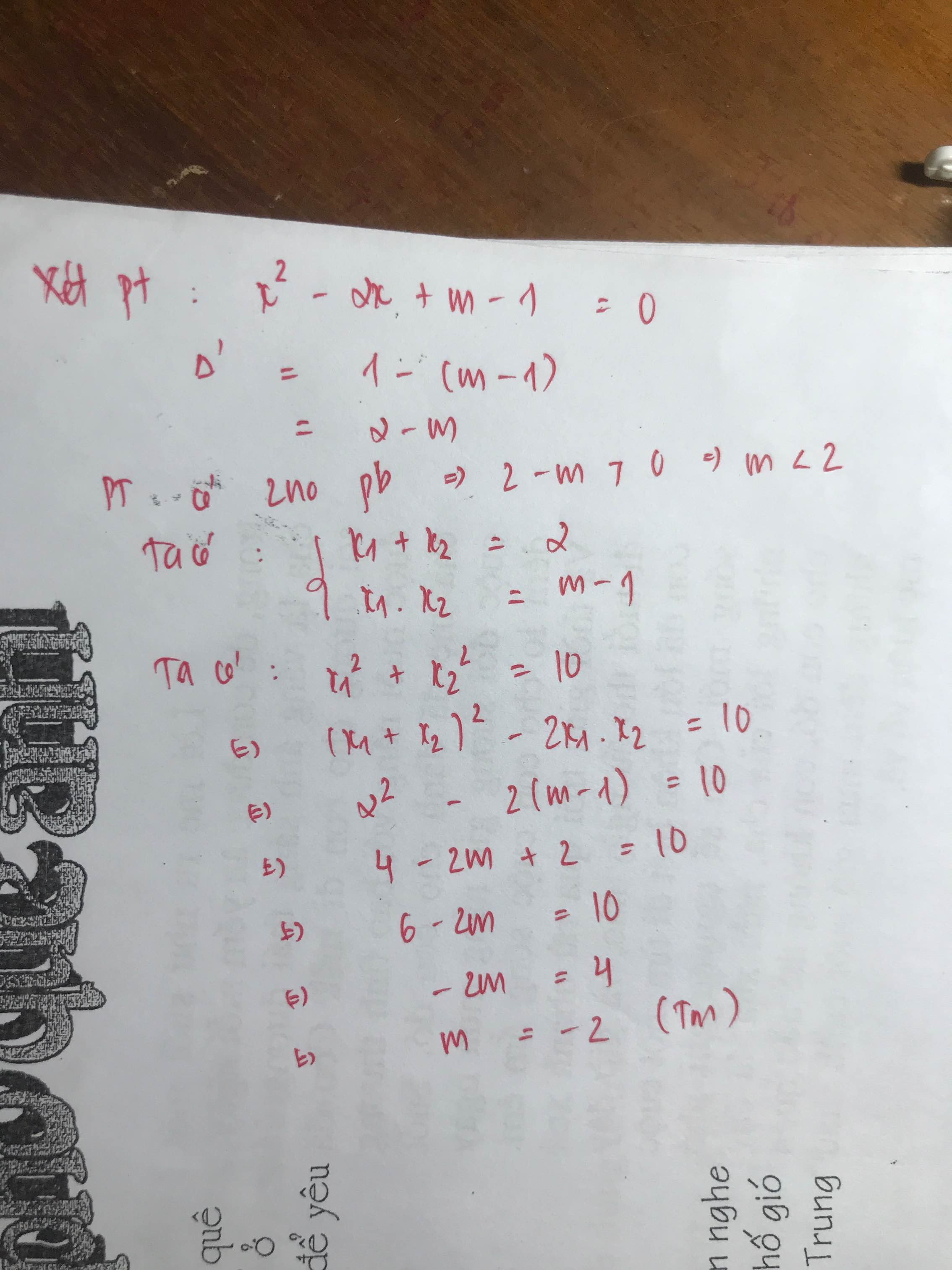
Áp dụng hệ thức Vi-ét,ta có :
\(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-2\end{cases}}\)
Ta có : \(x_1^2+x_2^2-3x_1x_2=14\Leftrightarrow\left(x_1+x_2\right)^2-5x_1x_2=14\)
\(\Leftrightarrow m^2+10=14\Rightarrow m^2=4\Rightarrow m=\pm2\)
Theo vi-ét \(\hept{\begin{cases}x_1+x_2=\frac{-b}{a}=m\\x_1.x_2=\frac{c}{a}=-2\end{cases}}\)
Thay vào ta có : \(x_1^2+x_2^2-3.x_1.x_2=14\)
\(< =>x_1^2+2.x_1.x_2+x_2^2-5.x_1.x_2=14\)
\(< =>\left(x_1+x_2\right)^2-5.x_1.x_2=14\)
\(< =>m^2-5.\left(-2\right)=m^2+10=14< =>\orbr{\begin{cases}m=2\\m=-2\end{cases}}\)
Cách mình ko khác anh Tùng tí nào đâu