Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

phương trình (E) có dạng:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Vì (E) đi qua điểm M nên
\(\dfrac{\dfrac{9}{5}}{a^2}+\dfrac{\dfrac{16}{5}}{b^2}=1\)
\(\dfrac{9}{a^2}+\dfrac{16}{b^2}=5\)(1)
Do tam giác \(MF_1F_2\)vuông tại M
Nên M thuộc đường tròn \(x^2+y^2=c^2\)
\(\dfrac{9}{5}+\dfrac{16}{5}=c^2\)
\(5=c^2\)
\(a^2-b^2=5\)
\(a^2=5+b^2\)
Thế vào pt(1)
\(9b^2+16a^2=5a^2b^2\)
\(9b^2+16\left(5+b^2\right)=5b^2\left(5+b^2\right)\)
\(5b^4-80=0\)
\(b^2=\pm4\)
\(\Rightarrow b^2=4\Rightarrow a^2=9\)
\(\left(E\right):\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
\(\Rightarrow c=\sqrt{5};e=\dfrac{\sqrt{5}}{2}\)

Phương trình chính tắc của elip có dạng: +
= 1
a) Elip đi qua M(0; 3):
+
= 1 => b2 = 9
Elip đi qua N( 3; ):
+
= 1 => a2 = 25
Phương trình chính tắc của elip là : +
= 1
b) Ta có: c = √3 => c2 = 3
Elip đi qua điểm M(1; )
+
= 1 =>
+
= 1 (1)
Mặt khác: c2 = a2 – b2
=> 3 = a2 – b2 => a2 = b2 + 3
Thế vào (1) ta được : +
= 1
<=> a2 = 4b2 + 5b2 – 9 = 0 => b2= 1; b2 = ( loại)
Với b2= 1 => a2 = 4
Phương trình chính tắc của elip là : +
= 1.

Phương trình chính tắc của elip có dạng :
+
= 1
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
Vậy phương trình chính tắc của elip có dạng +
= 1
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 – 9 = 16
Vậy phương trình chính tắc của elip có dạng +
= 1

\(\Leftrightarrow2m.2^x+\left(2m+1\right)\left(3-\sqrt{5}\right)^x+\left(3+\sqrt{5}\right)^x=0\)
\(\Leftrightarrow\left(\frac{3+\sqrt{5}}{2}\right)^x+\left(2m+1\right)\left(\frac{3-\sqrt{5}}{2}\right)^x+2m< 0\)
Đặt \(t=\left(\frac{3+\sqrt{5}}{2}\right)^x,0< t\le1\Rightarrow\frac{1}{t}=\left(\frac{3-\sqrt{5}}{2}\right)^x\)
Phương trình trở thành :
\(t+\left(2m+1\right)\frac{1}{t}+2m=0\) (*)
a. Khi \(m=-\frac{1}{2}\) ta có \(t=1\) suy ra \(\left(\frac{3+\sqrt{5}}{2}\right)^x=1\Leftrightarrow x=0\)
Vậy phương trình có nghiệm là \(x=0\)
b. Phương trình (*) \(\Leftrightarrow t^2+1=-2m\left(t+1\right)\Leftrightarrow\frac{t^2+1}{t+1}=-2m\)
Xét hàm số \(f\left(t\right)=\frac{t^2+1}{t+1};t\in\)(0;1]
Ta có : \(f'\left(t\right)=\frac{t^2+2t+1}{\left(t+1\right)^2}\Rightarrow f'\left(t\right)=0\Leftrightarrow=-1+\sqrt{2}\)
t f'(t) f(t) 0 1 0 - + 1 1 -1 + căn 2 2 căn 2 - 2
Suy ra phương trình đã cho có nghiệm đúng
\(\Leftrightarrow2\sqrt{2}-2\le-2m\le1\Leftrightarrow\sqrt{2}-1\ge m\ge-\frac{1}{2}\)
Vậy \(m\in\left[-\frac{1}{2};\sqrt{2}-1\right]\) là giá trị cần tìm

a) (E) có tiêu điểm \({F_1}\left( { - \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3\).
Phương trình chính tăc của (E) có dạng
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có: \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\(\Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\ (1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{ & {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr & \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr}\)
\(\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta\) đi qua điểm\(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3\).
Phương trình tung độ giao điểm của \(\Delta\) và \((E)\) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}\)
Suy ra tọa độ của C và D là :
\(C\left( {\sqrt 3 ; - {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.

a) \(\left(E\right):\dfrac{x^2}{5}+\dfrac{y^2}{4}=1\)
b) \(\left(E\right):\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\)
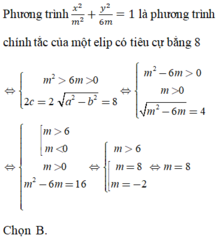



Đáp án C