


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(x\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(x\sqrt{x}\left(x-1\right)^2=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
B là đáp án đúng

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

c) x^2 -x-20=0
⇔x2−5x+4x−20=0⇔x2−5x+4x−20=0
⇔(x2+4x)−(5x+20)=0⇔(x2+4x)−(5x+20)=0
⇔x(x+4)−5(x+4)=0⇔x(x+4)−5(x+4)=0
⇔(x+4)(x−5)=0⇔(x+4)(x−5)=0
⇔[x+4=0x−5=0⇔[x=−4x=5⇔[x+4=0x−5=0⇔[x=−4x=5
Vậy...

Chọn B
TH1.Nếu a-1=0 hay a =1 thì
(1) thành: 2 > 0 ( luôn đúng mọi x) Tập nghiệm của bất phương trình T = R
(2) thành: 2x+1> 0 hay x> -1/2 Tập nghiệm của bất phương trình 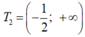
Vậy a= 1 không thỏa yêu cầu bài toán.
TH2. Nếu a+1= 0 hay a= -1thì
(1) thành: -2x=4>0 hay x< 2. Tập nghiệm của bất phương trình T2 = (-∞; 2)
(2) thành: 3> 0 luôn đúng Tập nghiệm của bất phương trình T= R
Vậy a= -1 không thỏa yêu cầu bài toán.
TH3. 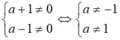
(1) : (a-1) x> a-3 và (2) : (a+1) x> a-2
Hai bất phương trình tương đương
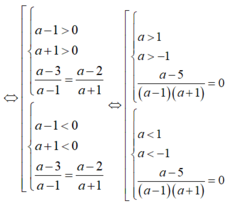
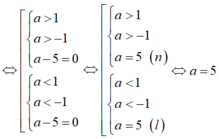

3x - 2(y - x + 1) > 0 ⇔ 3x - 2y + 2x - 2 > 0 ⇔ 5x - 2y - 2 > 0
Đáp án là B.

\(\Leftrightarrow2m.2^x+\left(2m+1\right)\left(3-\sqrt{5}\right)^x+\left(3+\sqrt{5}\right)^x=0\)
\(\Leftrightarrow\left(\frac{3+\sqrt{5}}{2}\right)^x+\left(2m+1\right)\left(\frac{3-\sqrt{5}}{2}\right)^x+2m< 0\)
Đặt \(t=\left(\frac{3+\sqrt{5}}{2}\right)^x,0< t\le1\Rightarrow\frac{1}{t}=\left(\frac{3-\sqrt{5}}{2}\right)^x\)
Phương trình trở thành :
\(t+\left(2m+1\right)\frac{1}{t}+2m=0\) (*)
a. Khi \(m=-\frac{1}{2}\) ta có \(t=1\) suy ra \(\left(\frac{3+\sqrt{5}}{2}\right)^x=1\Leftrightarrow x=0\)
Vậy phương trình có nghiệm là \(x=0\)
b. Phương trình (*) \(\Leftrightarrow t^2+1=-2m\left(t+1\right)\Leftrightarrow\frac{t^2+1}{t+1}=-2m\)
Xét hàm số \(f\left(t\right)=\frac{t^2+1}{t+1};t\in\)(0;1]
Ta có : \(f'\left(t\right)=\frac{t^2+2t+1}{\left(t+1\right)^2}\Rightarrow f'\left(t\right)=0\Leftrightarrow=-1+\sqrt{2}\)
t f'(t) f(t) 0 1 0 - + 1 1 -1 + căn 2 2 căn 2 - 2
Suy ra phương trình đã cho có nghiệm đúng
\(\Leftrightarrow2\sqrt{2}-2\le-2m\le1\Leftrightarrow\sqrt{2}-1\ge m\ge-\frac{1}{2}\)
Vậy \(m\in\left[-\frac{1}{2};\sqrt{2}-1\right]\) là giá trị cần tìm

a) \(x+2=0\Leftrightarrow x=-2\)
Phương trình: \(\dfrac{mx}{x+3}=3m-1\) (*) có đkxđ: \(x\ne-3\)
Vì cặp phương trình tương đương nên phương trình (*) có nghiệm là x = -2:
\(\dfrac{2m}{2+3}+3m-1=0\) \(\Leftrightarrow\dfrac{2m}{5}+3m=1\)\(\Leftrightarrow m\left(\dfrac{2}{5}+3\right)=1\)
\(\Leftrightarrow\dfrac{17}{5}m=1\) \(m=\dfrac{5}{17}\)
Vậy \(m=\dfrac{5}{17}\) thì hai phương trình tương đương.
b) Pt (1) \(x^2-9=0\) có hai nghiệm là: \(x=3;x=-3\).
Để cặp phương trình tương đương thì phương trình (2) \(2x^2+\left(m-5\right)x-3\left(m+1\right)=0\) có nghiệm là: \(x=3;x=-3\).
Suy ra: \(\left\{{}\begin{matrix}2.3^2+\left(m-5\right).3-3.\left(m+1\right)=0\\2.\left(-3\right)^2+\left(m-5\right).\left(-3\right)-3.\left(m+1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0=0\\30-6m=0\end{matrix}\right.\) \(\Leftrightarrow m=5\)
Vậy m = 5 thì hai phương trình tương đương.