Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Điều kiện cos x ≠ 0 cos x + π 4 ≠ 0
tan x + tan x + π 4 = 1 ⇔ tan x + tan x + 1 1 − tan x − 1 = 0
⇔ − tan 3 x + 3 tan x 1 − tan x = 0 ⇔ tan x ≠ 1 tan x 3 − tan x = 0 ⇔ tan x = 0 tan x = 3
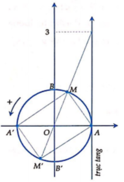
Ta có biểu thị các họ nghiệm của phương trình trẻn đường trọn lượn giác như hình bên.
Vậy đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình tan x + tan x + π 4 = 1 là tứ giác A M A ' M ' .
Cách 1: Đường thẳng có phương trình y = 3 x ⇔ 3 x − y = 0 .Khoảng cách từ điểm A 1 ; 0 đến M M ' là 3.1 − 0 3 2 + 1 2 = 3 10 . Do đó diện tích tứ giác A M A ' M ' là
S A M A ' M ' = 2 S A M M ' = 2. 1 2 . M M ' . d A , M M ' = 2. 3 10 ≈ 2.0,949
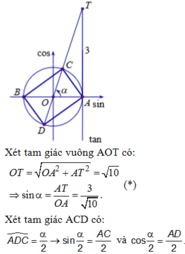
Cách 2: Ta có sin M O A ^ = 3 3 2 + 1 2 = 3 10
⇒ S A M A ' M ' = 4. S M O A = 4. 1 2 . O M . O A . sin M O A ^ = 2. 3 10 ≈ 2.0,949
Ta chọn D, do chỉ có 0,949 gần 2.0,949 nhất.

Đáp án D
Các họ nghiệm được biểu diễn bởi hai điểm A và C làm cho sin 3x = 0 và sin x = 0, do đó cot 3x và cot x không xác định.


+) Giải phương trình, biểu diễn các họ nghiệm trên đường tròn lượng giác.
+) Xác định các điểm và tính diện tích đa giác đó.
Cách giải:

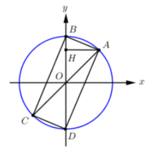
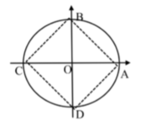
Biểu diễn hai họ nghiệm trên trên đường tròn lượng giác ta được
4 điểm A, B, C, D như sau:

Chú ý: Chú ý đối chiếu điều kiện xác định để loại nghiệm.

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

BÀI TOÁN PHỤ: CHứng minh rằng số chính phương lẻ chia cho 8 dư 1.
Giải: Xét số chính phương lẻ là \(m^2\left(m\in Z\right)\)
Như vậy m là số lẻ, đặt \(m=2n+1\)
Ta có:
\(m^2=\left(2n+1\right)^2=4n^2+4n+1=4.n.\left(n+1\right)+1\)
Vì n(n+1) là tích 2 số nguyên liên tiếp nên chia hết cho 2
\(\Rightarrow4n\left(n+1\right) \) chia hết cho 8
\(\Rightarrow4.n.\left(n+1\right)+1\) chia 8 dư 1
Vậy ta có điều phải chứng minh.
Vì a lẻ nên \(a\ne0\), phương trình \(ax^2+bx+c=0\) là phương trình bậc hai.
Xét \(\Delta=b^2-4ac\): b lẻ, theo bài toán phụ có \(b^2=8k+1\left(k\in Z\right)\)
a,c lẻ \(\Rightarrow\) \(ac\) lẻ
Đặt \(ac=2l-1\left(l\in Z\right)\)
Do đó \(\Delta=b^2-4ac=8k+1-4.\left(2l-1\right)=8k+1-8l+4=8\left(k-l\right)+5 \)chia cho 8 dư 5, theo bài toán phụ trên ta có \(\Delta\) không phải số chính phương.
\(\Delta\) là số nguyên, không phải óố chính phương \(\Rightarrow\sqrt{\Delta}\) là số vô tỉ
Nghiệm của phương trình đã cho (nếu có) là: \(x=\frac{-b\pm\sqrt{\Delta}}{2a}\)
b,a\(\in Z\), \(\sqrt{\Delta}\) vô tỉ nên x là vô tỉ.
Vậy phương trình có nghiệm nếu có thì các nghiệm ấy không thể là số hữu tỉ.
ơng là phươngax2+bx+c=0

a) ĐK: x-1 khác 0 và x+1 khác 0
<=> x khác 1 và x khác -1
b) ĐK: x-2 khác 0
<=> x khác 2
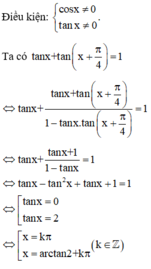


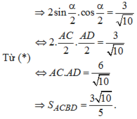
Đáp án B
Điều kiện: cos x ≠ 0 tan x ≠ 1
Ta có:
tan x + tan x + π 4 = 1 ⇔ tan x + tan x + tan π 4 1 − tan x . tan π 4 = 1
⇔ tan x + tan x + 1 1 − tan x = 1 ⇔ tan x − tan 2 x + tan x + 1 = 1 ⇔ tan x = 0 tan x = 2 ⇔ x = k π x = arctan 2 + k π k ∈ ℤ
suy ra 4 nghiệm trên đường tròn lượng giác là x = 0 x = π và x = arctan 2 x = arctan 2 + π
Vậy diện tích cần tính là S = 0 , 948