Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phân tích: Phương trình hoàn độ giao điểm:
\(x^2+2x-3=x+m\Leftrightarrow x^2+x-3-m=0\left(1\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại 2 điểm phân biệt A ; B
=> (1) có 2 nghiệm phân biệt
<=> \(\Delta>0\) \(\Leftrightarrow m>\dfrac{-13}{4}\left(2\right)\)
giả sử: \(A\left(x_1;y_1\right),B\left(x_2;y_2\right)\) với \(x_1;x_2\) là hai nghiệm của (1) Ta phải có :
\(\left(y_1-1\right)\left(y_2-2\right)< 0\Leftrightarrow\left(x_1+m-1\right)\left(x_2+m-1\right)< 0\)
\(\Leftrightarrow x_1x_2+\left(m-1\right)\left(x_1+x_2\right)+m^2-2m+1< 0\)
\(\Leftrightarrow m^2-4m-1< 0\Leftrightarrow2-\sqrt{5}< m< 2+\sqrt{5}\left(thỏa\left(2\right)\right)\)
\(m\in Z\Rightarrow m\in\left\{0;1;2;3;4\right\}\)

Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)

Phương trình hoành độ giao điểm: - x 2 + 2 x + 3 = m x ⇔ x 2 + m - 2 x - 3 = 0 1
Dễ thấy (1) luôn có 2 nghiệm phân biệt vì a c = 1 . - 3 = - 3 < 0
Khi đó (d) cắt (P) tại hai điểm phân biệt A x 1 ; m x 1 , B x 2 ; m x 2 , với x 1 , x 2 là nghiệm phương trình (1). Theo Viét, có: x 1 + x 2 = 2 - m , x 1 x 2 = - 3 x 1 x 2 = - 3
I là trung điểm
A B ⇒ I = x 1 + x 2 2 ; m x 1 + m x 2 2 = 2 − m 2 ; − m 2 + 2 m 2
Mà I ∈ ( Δ ) : y = x − 3 ⇒ − m 2 + 2 m 2 = 2 − m 2 − 3 ⇔ m 2 − 3 m − 4 = 0
⇔ m = − 1 = m 1 m = 4 = m 2 ⇒ m 1 + m 2 = 3
Đáp án cần chọn là: D

- Xét phương trình hoành độ giao điểm :\(x^2-2x+2=x+m\)
\(\Leftrightarrow x^2-3x+2-m=0\)
Có \(\Delta=b^2-4ac=9-4\left(2-m\right)=9-8+4m=4m+1\)
- Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta>0\) \(\Leftrightarrow m>-\dfrac{1}{4}\left(1\right)\)
Theo viet : \(\left\{{}\begin{matrix}x_a+x_b=3\\x_ax_b=2-m\end{matrix}\right.\)
- Ta có : \(OA^2+OB^2=10\)
\(\Leftrightarrow x^2_A+y^2_A+x_B^2+y^2_B=10\)
\(\Leftrightarrow x^2_a+x^2_b+\left(x_a+m\right)^2+\left(x_b+m\right)^2=10\)
\(\Leftrightarrow2x^2_a+2x^2_b+2m\left(x_a+x_b\right)+2m^2=10\)
\(\Leftrightarrow2\left(x_a+x_b\right)^2-4x_ax_b+2m\left(x_a+x_b\right)+2m^2-10=0\)
\(\Leftrightarrow18-4\left(2-m\right)+6m+2m^2-10=0\)
\(\Leftrightarrow2m^2+10m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-5\end{matrix}\right.\)
- Kết hợp ĐK (1) => m = 0 ( TM )
Vậy ...

Để (Pm) là đồ thị của hàm số bậc hai thì m-1<>0
hay m<>1
Phương trình hoành độ giao điểm là:
\(\left(m-1\right)x^2+\left(2m-4\right)x-5-4x+m=0\)
\(\Leftrightarrow\left(m-1\right)x^2+\left(2m-8\right)x+m-5=0\)
\(\text{Δ}=\left(2m-8\right)^2-4\left(m^2-6m+5\right)\)
\(=4m^2-32m+64-4m^2+24m-20\)
\(=-8m+44\)
Để phương trình có hai nghiệm phân biệt thì -8m+44>0
=>-8m>-44
hay m<11/2
Theo đề, ta có: \(\left(x_1+x_2\right)^2-4x_1x_2=4\)
\(\Leftrightarrow\dfrac{\left(2m-8\right)^2}{\left(m-1\right)^2}-4\cdot\dfrac{m-5}{m-1}=4\)
\(\Leftrightarrow\left(2m-8\right)^2-4\left(m^2-6m+5\right)=4\left(m-1\right)^2\)
\(\Leftrightarrow4m^2-32m+64-4m^2+24m-20=4\left(m^2-2m+1\right)\)
\(\Leftrightarrow4m^2-8m+4-8m-44=0\)
\(\Leftrightarrow4m^2-16m-40=0\)
\(\Leftrightarrow m^2-4m-10=0\)
\(\Leftrightarrow\left(m-2\right)^2=14\)
hay \(m\in\left\{\sqrt{14}+2;-\sqrt{14}+2\right\}\)

Phương trình hoành độ giao điểm: x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0
(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4
Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2
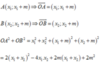
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4
Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2 khi m = − 5 2
Đáp án cần chọn là: A

Lời giải:
PT hoành độ giao điểm:
\(x^2+4x-3-(-mx-3)=0\)
\(\Leftrightarrow x^2+x(4+m)=0\)
\(\Leftrightarrow x(x+4+m)=0\)
\(\Rightarrow \left[\begin{matrix} x=0\\ x=-(m+4)\end{matrix}\right.\)
Để 2 đths cắt nhau tại hai điểm pb thì \(-(m+4)\neq 0\leftrightarrow m\neq -4\)
Khi đó 2 điểm A,B là: \(A(0; -3); B(-m-4, m^2+4m-3)\)
Để trung điểm $I$ của $AB$ nằm trên trục $Ox$ thì \(y_I=0\)
\(\Leftrightarrow \frac{y_A+y_B}{2}=0\)
\(\Leftrightarrow \frac{-3+m^2+4m-3}{2}=0\)
\(\Leftrightarrow m^2+4m-6=0\Rightarrow m=-2\pm \sqrt{10}\)
Phương trình hoành độ giao điểm:
\(x^2-x-m+2=x+4\Leftrightarrow x^2-2x-m-2=0\) (1)
Khi đó nghiệm \(x_1;x_2\) của (1) là hoành độ của A và B
\(\Rightarrow x_M=\dfrac{x_A+x_B}{2}=\dfrac{x_1+x_2}{2}=-\dfrac{-2}{2}=1\)
Do \(M\in d\Rightarrow y_M=x_M+4=1+4=5\)
Vậy tọa độ của M là \(M\left(1;5\right)\)