FZ
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 8 2020
a) Vì p là số nguyên tố lớn hơn 3 nên p chia cho 3 dư 1 hoặc 2
+) \(p\equiv2\left(mod3\right)\)
\(\Rightarrow p+4\equiv6\left(mod3\right)\equiv0\left(mod3\right)\)
\(\Rightarrow p+4⋮3\)
Mà \(p+4>3\) nên \(p+4\) là hợp số (loại)
\(\Rightarrow p\equiv1\left(mod3\right)\)
\(\Rightarrow p+8\equiv9\left(mod3\right)\)
\(\Rightarrow p+8⋮3\)
Vì p + 8 > 3
\(\Rightarrow\)p + 8 là hợp số (đpcm)
b) (d + 2c + 4b) như thế mới đúng chứ nhỉ?!
Ta có: \(\overline{abcd}=1000a+100b+10c+d\)
\(=4b+2c+d+1000a+96b+8c\)
Mà \(1000a⋮8\); \(96b⋮8\)và \(8c⋮8\)
\(\Rightarrow4b+2c+d⋮8\)
\(\Rightarrow\overline{abcd}⋮8\) (đpcm)
16 tháng 8 2020
Nếu bạn thấy mình làm khó hiểu câu a thì để mình làm cách khác
Vì p là số nguyên tố lớn hơn 3 nên p có dạng 3k+1 hoặc 3k+2 với k là số tự nhiên khác 0
Với p = 3k + 2
=> p + 4 = 3k + 6 chia hết cho 3
p + 4 > 3 => p + 4 là hợp số
=> p = 3k + 2 (loại)
=> p = 3k + 1
=> p + 8 = 3k + 9 chia hết cho 3
Mà p + 8 > 3 nên p + 8 là hợp số (đpcm)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
17 tháng 5 2016
Ta có:
abcd = 1000a + 100b + 10c + d = 1000a + 96b + 4b + 8c + 2c + d = (1000a + 96b + 8c) + (d + 2c + 4b)
Mà d + 2c + 4b chia hết cho 8 theo đề bài
Và 1000a + 96b + 8c cũng chia hết cho 8
=> abcd chia hết cho 8
16 tháng 5 2016
a) Vì p là số nguyên tố lớn hơn 3
=> p có dạng 3k + 1 hoặc 3k + 2 ( k thuộc N*)
Nếu p có dạng 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 = 3 ( k + 2 ) là hợp số
=>p không có dạng 3k + 2
=>p có dạng 3k + 1
=> p + 8 = 3k + 1 + 8 = 3k + 9 = 3 ( k + 3 ) là hợp số ( đpcm )
b)
Ta có:
abcd =1000a + 100b + 10c + d = 1000a + 96b + 4b + 8c + 2c + d = ( 1000a + 96b + 8c ) + ( d + 2c + 4b ) = 8 ( 125a + 12b + c ) + ( d + 2c + 4b )
Vì 8 ( 125a + 12b + c ) chia hết cho 8
Mà ( d + 2c + 4b ) chia hết cho 8
=> 8 ( 125a + 12b + c ) + ( d + 2c + 4b ) chia hết cho 8
hay abcd chia hết cho 8 ( đpcm )
5 tháng 3 2017
Vì \(p>3\) nên p không chia hết cho 3 khi đó p có dạng
\(3k+1\) hoặc \(3k+2\) \(k\in N\)
\(\cdot\)) Nếu \(p=3k+1\)
Nếu d chia 3 dư 1 thì \(p+2d⋮3\left(loai\right)\)
Vì p+2d là số nguyên tố nên loại
Vậy \(p=3k+1\) thì \(d⋮3\)
Tương tự với \(p=3k+2\) thì \(d⋮3\)
Vậy \(p>3\) và \(p;p+d;p+2d\) là các số nguyên tố thì \(p⋮3\left(1\right)\)
p lẻ p+d nguyên tố thì p+d lẻ nên d chẵn do đó \(d⋮2\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có \(d⋮6\)
25 tháng 7 2015
p là số nguyên tố > 3 => p lẻ
p + d là số nguyên tố => p + d lẻ mà p lẻ => d chẵn => d chia hết cho 2
+) Xét p = 3k + 1
Nếu d chia cho 3 dư 1 => d = 3m + 1 => p + 2d = 3k + 1 + 2. (3m +1) = 3k + 6m + 3 chia hết cho 3 => không là số nguyên tố
Nếu d chia cho3 dư 2 => d = 3m + 2 => p +d = 3k + 1 + 3m + 2 = 3k + 3m + 3 => p + d không là số nguyên tố
=> d chia hết cho 3
+) Xét p = 3k + 2
Nếu d chia cho 3 dư 1 => d = 3m + 1 => p + d = 3k + 2 + 3m + 1 = 3k + 3m + 3 => p + d không là số ngt
Nếu d chia cho 3 dư 2 => d = 3m + 2 => p + 2d = 3k + 6m + 6 => p + 2d không là số ngt
=> d chia hết cho 3
Vậy d chia hết cho cả 2 và 3 => d chia hết cho 6
4 tháng 3 2019
Vì p,p+d,p+2d là số nguyên tố >3 nên p,p+d,p+2d ko chia hết cho 3
=>p,p+d,p+2d khi : cho 3 thì có số dư là 1 và 2
=>trong 3 số p,p+d,p+2d có ít nhất 2 số có cùng số dư( định lí Đi-rec-lê thì phải (mk ko nhớ mấy))
+)nếu p và p+d cùng số dư =>(p+d)-p chia hết cho 3 hay d chia hết cho 3
+)nếu p và p+2d cùng số dư =>(p+2d)-p chia hết cho 3 hay 2d chia hết cho 3=> d chia hết cho 3 ( vì (2,3)=1)
+)nếu p+d và p+2d cùng số dư=>(p+2d)-(p+d) chia hết cho 3 hay p chia hết cho 3
=>d chia hết cho 3 (1)
Vì p,p+d,p+2d là số nguyên tố > 3 =>p,p+d,p+2d ko chia hết cho 2=>(p+d)-p chia hết cho 2 hay d chia hết cho 2 (2)
Từ (1) và (2)=> d chia hết cho 6 ( vì (2,3)=1)
22 tháng 12 2015
3) CM:p+1 chia hết cho 2
vì p lớn hơn 3 suy ra p là số lẻ và p+1 là số chẵn.
Vậy p+1 chia hết cho 2
CM:p+1 chia hết cho 3
Ta có:p x (p+1) x (p+2) chia hết cho 3(vì tích 3 số liên tiếp luôn chia hết cho 3)
Mà p và p+2 là số nguyên tố nên p và p+2 ko chia hết cho 3
Vậy p+1 chia hết cho 3
Mà ƯCLN(2,3) là 1
Vậy p+1 chia hết cho 2x3 là 6
Vậy p+1 chia hết cho 6 với mọi p lớn hơn 3 và p+2 cùng là số nguyên tố.
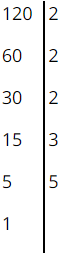
Vì p là số nguyên tố > 3 => p có dạng 3k + 1 hoặc 3k +2 ( k thuộc N)
+) Trường hợp: p = 3k + 1
Nếu d chia cho 3 dư 1 => d = 3n + 1 => p + 2d = 3k + 1 + 6n + 2 = 3k + 6n + 3 chia hết cho 3 (mâu thuẫn với p+ 2d là số nguyên tố)
Nếu d chia cho 3 dư 2 => d = 3n + 2 => p + d = 3k + 1 + 3n + 2 = 3k + 3n + 3 chia hết cho 3 (Mâu thuẫn)
Vậy d chia hết cho 3
+) Trường hợp : p = 3k + 2. Tương tự ta có: d chia hết cho 3
=> d chia hết cho 3
Mà p; p + d là số nguyên tố => lẻ => p+ d - p = d chẵn hay d chia hết cho 2
Vậy d chia hết cho cả 2 và 3 => d chia hết cho 6
Giả sử tồn tại các số nguyên x,y sao cho x^2+5=y^3.
Nếu x lẻ thì y chẵn, nhưng khi đó, x^2+5 chia 8 dư 6 còn y^3 chia hết cho 8, vô lí.
Nếu x chẵn thì y lẻ.
---Nếu y chia 4 dư 3 thì y^3 chia 4 dư 3, nhưng x^2+5 chia 4 dư 1, vô lí.
---Nếu y chia 4 dư 3 thì y^2+y+1 chia 4 dư 3
Suy ra x^2+4 =y^3 – 1 = (y – 1)(y^2+y+1) có ước nguyên tố dạng 4k+3, vô lí.
Vậy không tồn tại các số nguyên x,y sao cho x^2+5=y^3.