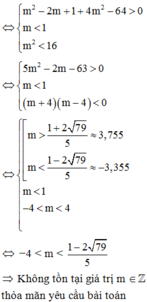Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét pt hoành độ gđ của parabol và d có:
\(x^2=x+m-1\)
\(\Leftrightarrow x^2-x+1-m=0\) (1)
Để (P) và (d) cắt nhau tại hai điểm pb bên trái trục tung
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S=1< 0\left(vl\right)\\P=1-m>0\end{matrix}\right.\)\(\Rightarrow\) Không tồn tại m để (d) cắt (P) tại hai điểm pb ở bên trái trục tung
Vậy...
Phương trình hoành độ giao điểm là:
\(x^2-x-m+1=0\)
a=1; b=-1; c=-m+1
\(\Delta=b^2-4ac\)
\(=\left(-1\right)^2-4\left(-m+1\right)\)
\(=1+4m-4\)
=4m-3
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow m>\dfrac{3}{4}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-1\right)}{1}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m+1}{1}=-m+1\end{matrix}\right.\)
Để (d) cắt (P) tại hai điểm phân biệt nằm ở bên trái trục tung thì
\(\left\{{}\begin{matrix}m>\dfrac{3}{4}\\x_1+x_2< 0\left(loại\right)\\x_1x_2>0\end{matrix}\right.\)
Vậy: \(m\in\varnothing\)

Phương trình hoành độ giao điểm x 2 = (m – 2)x + 3m ↔ x 2 − (m – 2)x − 3m = 0 (*)
Đường thẳng d cắt (P) tại hai điểm phân biệt nằm hai phía trục tung
↔ Phương trình (*) có hai nghiệm trái dấu
↔ ac < 0 ↔ −3m < 0 ↔ m > 0
Đáp án: D

a: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-1\right)x+m+4\)
=>\(x^2-\left(m-1\right)x-m-4=0\)(1)
a=1; b=-(m-1)=-m+1; c=-m-4
Để (P) cắt (d) tại hai điểm nằm về hai phía so với trục tung thì phương trình (1) có hai nghiệm trái dấu
=>1(-m-4)<0
=>m+4>0
=>m>-4
b: Để (P) cắt (d) tại hai điểm cùng nằm về phía bên trái trục Oy thì phương trình (1) có hai nghiệm phân biệt cùng âm
=>\(\left\{{}\begin{matrix}\Delta>0\\x_1x_2>0\\x_1+x_2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-m+1\right)^2-4\cdot1\cdot\left(-m-4\right)>0\\\dfrac{-\left(-m+1\right)}{1}< 0\\\dfrac{-m-4}{1}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-2m+1+4m+16>0\\m-1< 0\\m+4< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< 1\\m< -4\end{matrix}\right.\)
=>m<-4