Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ Phương trình hoành độ giao điểm sẽ tìm được tọa độ của A ( x1,y1) và B (x2 , y2)
Bạn Vẽ hình . Gọi M là hình chiếu của A trên Ox , N là Hình chiếu của B trên Ox . tiếp theo bạn tính lần lượt các diện tích sau.:
1. S tam giác AMO vuông tại M
2. S tam giác BNO vuông tại N
3. S Hình Thang AMNB .
=> S tam giác AOB = S Hình thang AMNB - ( S tam giác AMO + S tam giác BNO)

\(b,\text{PT giao Ox của }\left(d_2\right):y=0\Leftrightarrow-x+3=0\Leftrightarrow x=3\Leftrightarrow B\left(3;0\right)\Leftrightarrow OB=3\\ \text{PTHĐGĐ }\left(d_1\right)\text{ và }\left(d_2\right):2x=-x+3\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\\ \text{Gọi }H\text{ là đường cao từ }A\text{ của }\Delta OAB\\ \Rightarrow AH=\left|y_A\right|=2\\ \Rightarrow S_{OAB}=\dfrac{1}{2}AH\cdot OB=\dfrac{1}{2}\cdot2\cdot3=3\left(đvdt\right)\)

a) tự vẽ
b) pt hoành độ
x^2=x+2
giải ra được x1=...;x2=,,,,,
thay x1=...;x2=... vô y=x^2
ta được y1=...;y2=...
ta được A;B có vị trí A(x1;y1);B(x2;y2)

a/ Bạn tự vẽ
b/ Ta lập pt hoành độ giao điểm :
(d1) giao với (d2) : \(-x-5=\frac{1}{4}x\Leftrightarrow x=-4\) thay vào (d1) được y = -1
Vậy A(-4;-1) . Tương tự ta tìm được điểm B(-1;-4)
c/ Ta có : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(-1+4\right)^2+\left(-4+1\right)^2}=3\sqrt{2}\)
\(OA=\sqrt{x_A^2+y_A^2}=\sqrt{4^2+1^2}=\sqrt{17}\) ; \(OB=\sqrt{x_B^2+y_B^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
=> OAB là tam giác cân
d/ Gọi OH là đường cao hạ từ O xuống AB (H thuộc AB)
Vì tam giác OAB cân tại O nên AH = HB = 1/2AB = \(\frac{3\sqrt{2}}{2}\)
\(OH=\sqrt{OA^2-BH^2}=\sqrt{17-\left(\frac{3\sqrt{2}}{2}\right)^2}=\frac{5\sqrt{2}}{2}\)
\(S_{ABC}=\frac{1}{2}AB.OH=\frac{1}{2}.3\sqrt{2}.\frac{5\sqrt{2}}{2}=\frac{15}{2}\)

(d1): y = 1/2x + 2
và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
(d1) là đường thẳng đi qua hai điểm (0; 2) và (-4; 0)
(d2) là đường thẳng đi qua hai điểm (0; 2) và (2;0)
2. Tính chu vi và diện tích của tam giác ABC
(d1) và (d2) cùng cắt nhau tại một điểm trên trục tung có tung độ bằng 2
Áp dụng định lý Pi ta go cho các tam giác AOC và BOC vuông ở O ta được:
\(AC=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}\)
\(BC=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
Chu vi tam giác ABC : AC + BC + AB= 2√5 + 2√2 + 6
≈ 13,30
Diện tích tam giác ABC
\(\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6CM^2\)
NHÉ THAK NHÌU

a: 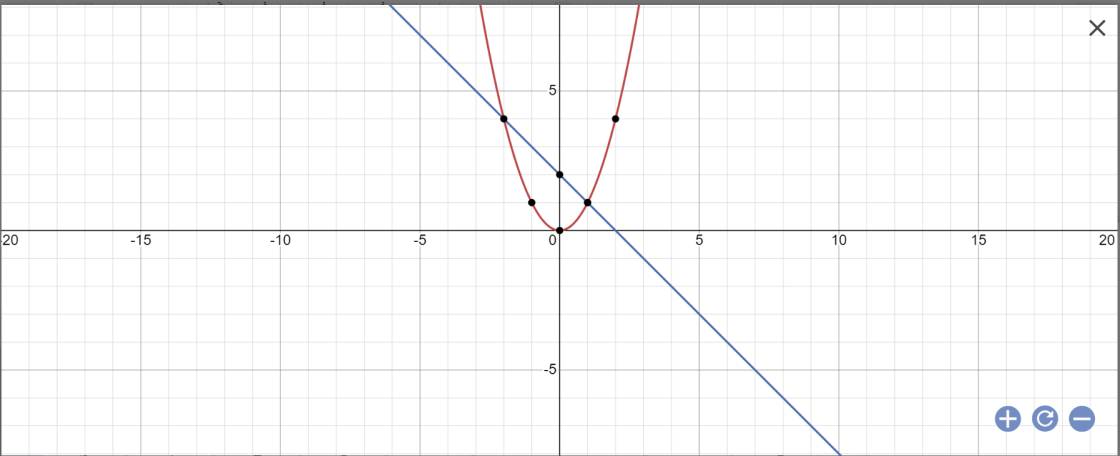
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1