Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

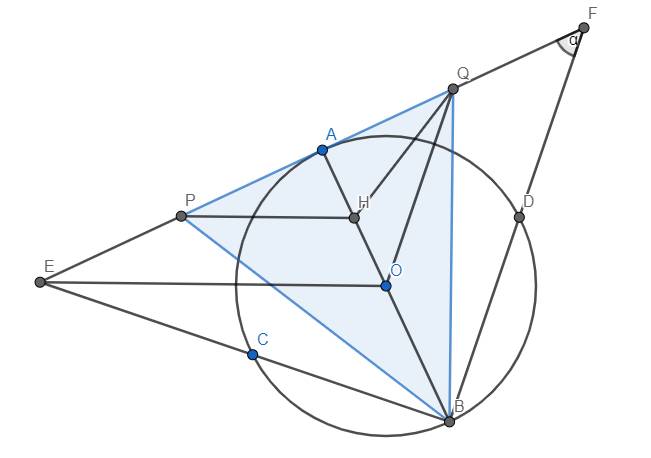
a) Định nghĩa lại H là trung điểm OA. Ta thấy OQ là đường trung bình của tam giác ABF nên OQ//BF. Hơn nữa \(BF\perp BE\) nên \(OQ\perp BE\). Lại có \(BA\perp QE\) nên O là trực tâm của tam giác BEQ \(\Rightarrow OE\perp BQ\)
Mặt khác, PH là đường trung bình của tam giác AOE nên PH//OA. Do đó, \(PH\perp BQ\). Lại thấy rằng \(BH\perp PQ\) nên H là trực tâm tam giác BPQ (đpcm)
b) Ta có \(P=\sin^6\alpha+\cos^6\alpha\)
\(=\left(\sin^2\alpha\right)^3+\left(\cos^2\alpha\right)^3\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^4\alpha+\cos^4\alpha-\sin^2\alpha\cos^2\alpha\right)\)
\(=1.\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-3\sin^2\alpha\cos^2\alpha\right]\)
\(=1-3\sin^2\alpha\cos^2\alpha\)
\(\le1-3.\dfrac{\left(\sin^2\alpha+\cos^2\alpha\right)^2}{4}\)
\(=\dfrac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\sin\alpha=\cos\alpha\) \(\Leftrightarrow\alpha=45^o\) hay 2 dây AB, CD vuông góc với nhau.
Vậy \(min_P=\dfrac{1}{4}\)
c) Ta có \(\left\{{}\begin{matrix}EC.EB=EA^2\\FD.FB=FA^2\end{matrix}\right.\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow EC.EB.FD.FB=\left(EA.FA\right)^2\)
\(\Rightarrow EC.FD.\left(EB.DB\right)=AB^4\)
\(\Rightarrow EC.FD.\left(EF.AB\right)=AB^4\)
\(\Rightarrow EC.FD.EF=AB^3=CD^3\) (đpcm)
Ta có \(EC.DF=AC.AD=BC.BD\)
\(\Rightarrow\dfrac{EC}{DF}=\dfrac{BC.BD}{DF^2}\)
\(=\dfrac{BC}{DF}.\dfrac{BD}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AC}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AE}{AF}\)
\(=\left(\dfrac{BE}{BF}\right)^3\)
Ta có đpcm.
Bài khá căng đấy

O A B C D E F
a, Xét \(\Delta\)CED có: OE = OD = OC ( = R)
=> \(\Delta\)CED vuông tại E
=> \(CE\perp DA\)
Vì AC là tiếp tuyến
\(\Rightarrow AC\perp CO\)
Xét \(\Delta\)ACD vuông tại C có CE là đường cao
DE . DA = CD2 = 4R2
b) Áp dụng định lí Pytago trong tam giác ACD có :
AD=(R3√)2+R2−−−−−−−−√ =2R.
tanAOCˆ=AC/OA=3√ ⇒AOCˆ=60o⇒AOBˆ=120o
⇒BDCˆ=60o⇒ΔOBDđều
Xét tam giác vuông ODF có : OFDˆ=30o
Có BOFˆ=90o−BODˆ=30o
⇒OFDˆ=BOFˆ⇒ΔOBFcân tại B ⇒BO=BF=BD⇒B là trung điểm của DF.
⇒ED=2BD=2R.
Tam giác FCD cân tại F nên FD=FC=2R.
Vậy OA=FC=2R.
Ta có ΔOBD đều ⇒DBOˆ=60o
Lại có BOAˆ=AODˆ=60o⇒BOAˆ=DBOˆ=60o
Mà hai góc này ở vị trí so le trong ⇒OA//DF.
Do đó tứ giác ODFA là hình bình hành ⇒OD//AF⇒OC//AF.
Tứ giác OCAF có : OC // AF (cmt)
AC // OF (cùng vuông góc OC)
=> OCAF là hình bình hành, lại có OA = FC (cmt) => OCAF là hình chữ nhât.
⇒SOCAF=OC.AC=R.R3√ =R2√3

DFCE nội tiếp
=>góc DFE=góc DCE=90 độ
ΔDOF đồng dạng với ΔDAB
=>DO/DA=DF/DB(1)
ΔOAB vuông tại B
=>OA^2=BO^2+BA^2
=>AB=Rcăn 3
=>DA=R căn 7
(1) =>R/Rcăn7=DF/2R
=>DF=2R/căn 7
Kẻ BH vuông góc DA
\(S_{ABD}=\dfrac{1}{2}\cdot BD\cdot AB=\dfrac{1}{2}\cdot BH\cdot DA\)
=>BH=2*Rcăn 3/căn 7
=>\(S_{BDF}=\dfrac{2R^2\sqrt{3}}{7}\)