Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét \(\left(O\right)\) có
OK là một phần đường kính
AB là dây
OK\(\perp\)AB tại K
Do đó: K là trung điểm của AB
Suy ra: \(AK=KB=\dfrac{AB}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAKO vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
\(\Leftrightarrow OK^2=5^2-4^2=9\)
hay OK=3cm
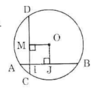
Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: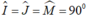 
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
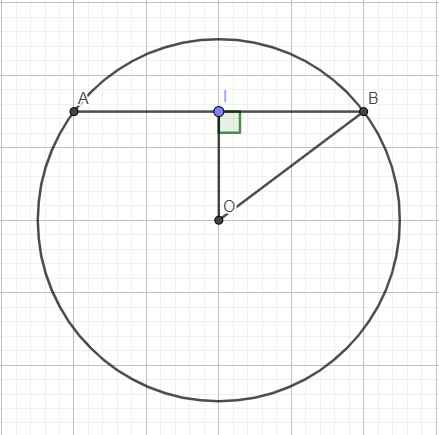
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
Ta có: \(IB=\dfrac{1}{2}AB=4\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông OIB:
\(OI^2+IB^2=OB^2\)
\(\Rightarrow OI=\sqrt{OB^2-IB^2}=\sqrt{5^2-4^2}=3\left(cm\right)\)
a: ΔOBC cân tại O có OH là đường cao
nên H là trung điểm của BC
=>HB=HC=8/2=4cm
ΔOHB vuông tại H nên OB^2=OH^2+HB^2
=>OH^2=5^2-4^2=9
=>OH=3cm
Xét ΔOHB vuông tại H có sin BOH=BH/BO=4/5
nên \(\widehat{BOH}\simeq53^0\)
b: Xét ΔABC có
AH vừa là đường cao, vừa là đường trung tuyến
=>ΔABC cân tại A
=>AB=AC
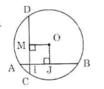
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
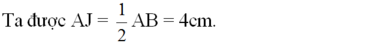
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: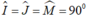 
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
