Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối O với H
Xét đg tròn (O), có:
OK∈ đg kính
K là td của HI (gt)
HI là dây không đi qua tâm
⇒OK⊥HI tại K
⇒HKI=90o
⇒ΔHKI vg tại K
Xét ΔHKI vg tại K, có:
HK2+OK2=OH2(ĐL Pi ta go)
Mà HK=8 cm (K là td của HI)
OH= 10cm (=R)
⇒OK2=36
⇒OK=6 cm (Vì OK>0)

a)vẽ hình
áp dụng định lý pitago ta có:AB=\(\sqrt{BC^2}-AC^2=\)\(5\sqrt{5}\)(cm)
tag C=AB/AC=5\(\sqrt{5}\)/5=\(\sqrt{5}\)/2
suy ra C=48 độ,B=42độ
b) tương tự
ok mik sẽ giải thích chi tiết cho bạn nha:còn hình ở phía dưới
áp dụng định lý pitago vào tam giác vuông ABC:
BC=\(\sqrt{AB^2+AC^2}=\sqrt{7^2+12^2}=\sqrt{193}\)
ta tìm tagC=\(\dfrac{7}{12}=0,58\)
sau đó ta bấm vào máy tính Casio là :SHIFT ,tag,0,58 máy tính hiện lên là 30,11
\(\Rightarrow C=30.11độ\) B=180-90-30,11=59,89
mà giải tam giác nghĩa là tìm các cạch và các góc còn thiếu của tam giác đó

Xét \(\left(O\right)\) có
OM là một phần đường kính
AB là dây
M là trung điểm của AB
Do đó: OM\(\perp\)AB tại M
Ta có: M là trung điểm của AB
nên \(AM=BM=\dfrac{AB}{2}=8cm\)
Áp dụng định lí Pytago vào ΔOMA vuông tại M, ta được:
\(OM^2+MA^2=OA^2\)
\(\Leftrightarrow OM^2=36\)
hay OM=6cm

Câu 1
1) ĐKXĐ: \(x\ge0;x\ne9\)
Thay \(x=16\) ( Thỏa mãn điều kiện ) vào biểu thức \(A\) ta được:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}=\dfrac{\sqrt{16}}{\sqrt{16}+3}=\dfrac{4}{4+3}=\dfrac{4}{7}\)
Vậy \(A=\dfrac{4}{7}\) khi \(x=16\)
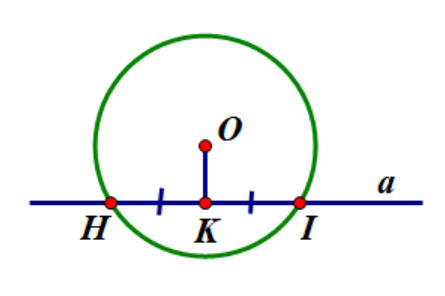
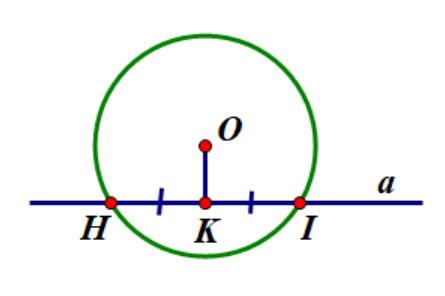 Cho (O;10cm) và dây HI = 16cm. Tính OK = ?
Cho (O;10cm) và dây HI = 16cm. Tính OK = ?