Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

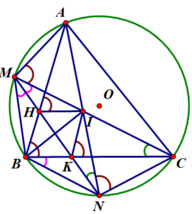
3) Chứng minh tứ giác BHIK là hình thoi.
Ta có A B C ^ = A N C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
Mà A M C ^ = A H I ^ (góc nội tiếp cùng chắn cung I C ⏜ )
⇒ A B C ^ = I K C ^ Mà 2 góc này ở vị trí đồng vị nên H B / / I K (1)
+ Chứng minh tương tự phần 1 ta có tứ giác AMHI nội tiếp
A N C ^ = I K C ^ (góc nội tiếp cùng chắn cung A I ⏜ )
Ta có A B C ^ = A M C ^ (góc nội tiếp cùng chắn cung A C ⏜ )
⇒ A B C ^ = A H I ^ Mà 2 góc này ở vị trí đồng vị nên B K / / H I (2)
Từ (1) và (2) suy ra tứ giác BHIK là hình bình hành.
Mặt khác AN, CM lần lượt là các tia phân giác của các góc A và C trong tam giác ABC nên I là giao điêm 3 đường phân giác, do đó BI là tia phân giác góc B
Vậy tứ giác BHIK là hình thoi (dấu hiệu nhận biết hình thoi).

a) CM: tứ giác BMHI nội tiếp
Có: NMC^ = (1/2) * sđ cung NC = (1/2) * sđ cung NA = NBA^
=> NMC^ = NBA^ => HMI^ = HBI^ => tứ giác BMHI nội tiếp đtròn
b) CM: MK * MN = MI * MC
Chứng minh tương tự câu a, ta được: tứ giác IKNC nội tiếp đtròn => NCI^ = IKM^
=> NCM^ = IKM^
=> hai tam giác NCM đồng dạng tam giác IKM (M^ chung; NCM^ = IKM^)
=> MN/ MI = MC/MK => MK* MN= MI * MC
c) CM: tam giác AKI cân tại K và tứ giác AHIK là h.thoi
* Có: IKH^ = NCI^ (tứ giác IKNC nt đtròn, c/m câu b)
= NCM^
= NBM^ (cùng chắn cung MN của (O))
= IBM^
= IMH^ (tứ giác BMHI nt đtròn)
=> IKH^ = IMH^ => tam giác KIH cân tại I
=> IK = IH (1)
Mặt khác, MN là đường phân giác ANI^ và AMI^ ;
MN là đường trung trực đoạn AI
mà H,K thuộc MN
=> HK là đường trung trực đoạn AI
=> KA=KI và HA=HI (t/c đối xứng) (2)
(1) và (2) => KA = KI = HI=HA
=> tam giác AKI cân tại K (KA=KI)
và tứ giác AHIK là h.thoi

a) góc BMN = góc ACN => đpcm
b) góc MKC = sđ BN + sđ MC = sđ AN+ sđ AM = góc NCM => đpcm
c) góc ABK= góc CBK => BK là đg p.g
tg tự CK là đg p.g
=>đpcm