Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình tự vẽ nhe
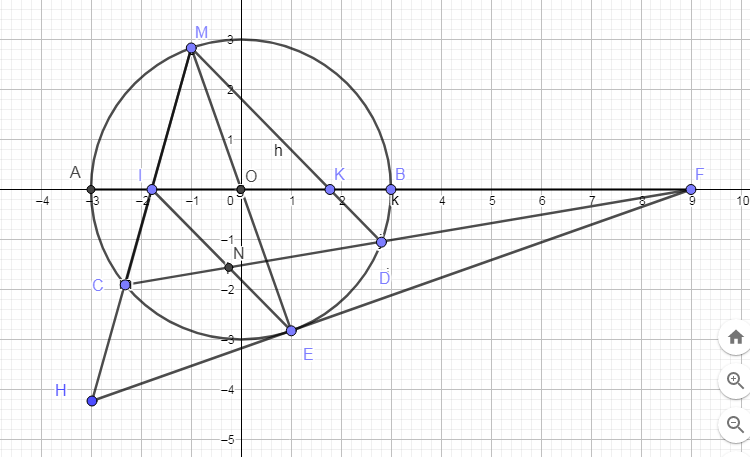
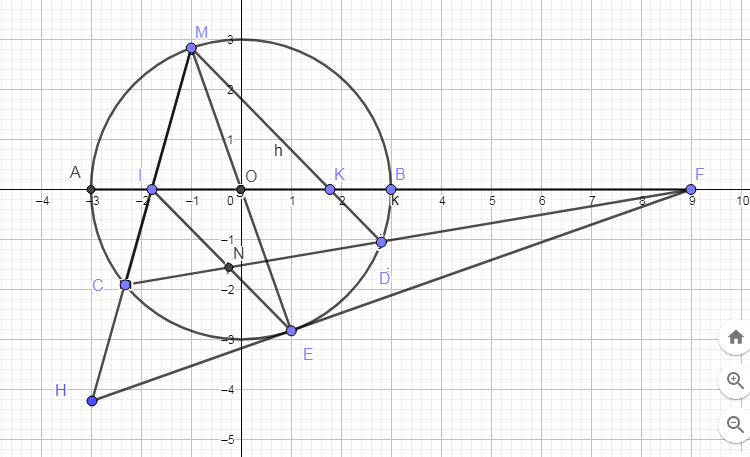
a, \(DE\perp MD\)( ME là đường kính )
mà \(\left\{{}\begin{matrix}ED//HN\left(cmt\right)\\MD//EI\left(EIMK:hbh\right)\end{matrix}\right.\)
=> HN⊥EI
mà EC ⊥MC ( ME là đường kính)
khi đó : CN cùng nhìn với EH dưới góc vuông
Vậy ENCH nội tiếp.( đpcm)
b, gọi điểm giao nhau giữa FD và MH là G
ta có :
góc HNG = góc HEG ( ENCH nội tiếp)
góc EDG = góc HNG ( đồng vị)
từ đó suy ra:
góc HEG = góc EDG
<=> góc HEG là góc giữa tiếp tuyến và dây cung
hay nói cách khác: EF là tiếp tuyến của (O)( đpcm)

Bài này bạn từng gửi rồi phải không nhỉ? Bạn tham khảo câu trả lời tại đây nghen
https://hoc24.vn/cau-hoi/cho-o-duong-kinh-abhai-diem-ik-thuoc-ab-sao-cho-oiokm-bat-ki-thuoc-omomimk-cat-o-lan-luot-tai-ecd-cat-ab-tai-fei-cat-df-tai-nmi-cat-e.4642078897220

Tứ giác MKEI là hình bình hành (2 đường chéo cắt nhau tại trung điểm mỗi đường)
\(\Rightarrow KD||IN\Rightarrow\dfrac{FK}{FI}=\dfrac{FD}{FN}\) (Talet)
\(KE||IH\Rightarrow\dfrac{FK}{FI}=\dfrac{FE}{FH}\)
\(\Rightarrow\dfrac{FD}{FN}=\dfrac{FE}{FH}\Rightarrow DE||HN\) (Talet đảo)
ME là đường kính \(\Rightarrow\widehat{MCE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow CE\perp CM\Rightarrow\widehat{HCE}=90^0\)
Tương tự ta có \(MD\perp DE\) , mà \(\left\{{}\begin{matrix}MD||NE\\DE||HN\end{matrix}\right.\) \(\Rightarrow NE\perp HN\)
\(\Rightarrow C\) và N cùng nhìn HE dưới 1 góc vuông nên ENCH nội tiếp

mình không vẽ hình nhé
a) \(\Delta ABD~\Delta AFE\left(g.g\right)\Rightarrow\frac{AB}{AF}=\frac{AD}{AE}\Rightarrow AB.AE=AD.AF\)
b) AM cắt BD tại H
Xét \(\Delta AEF\)có M là trung điểm EF
\(\Rightarrow AM=MF=ME\)
\(\Rightarrow\Delta AMF\)cân tại M
\(\Rightarrow\widehat{MAF}=\widehat{MFA}=\widehat{ABD}\)
Mà \(\widehat{ABD}+\widehat{ADB}=90^o\Rightarrow\widehat{MAF}+\widehat{ADB}=90^o\)
\(\Rightarrow\widehat{AHD}=90^o\Rightarrow AM\perp BD\)
c) vì AK là dây chung của hai đường tròn ( O ) và ( M ) nên \(OM\perp AK\)
Xét \(\Delta AMS\)có MO và AO là đường cao nên O là trực tâm
\(\Rightarrow SO\perp AM\)( 1 )
Mà \(BD\perp AM\)( 2 )
Từ ( 1 ) và ( 2 ) nên B,D,S thẳng hàng