Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
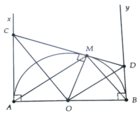
O A B C E D M
Ta thấy EB // AC nên \(\frac{EB}{MA}=\frac{ED}{DA}\Rightarrow AM.ED=EB.DA\) (1)
Do EB//AC nên \(\widehat{BCA}=\widehat{CBE}\Rightarrow\widebat{EC}=\widebat{CB}\)
Vậy thì \(2.\widehat{DMC}=\widebat{BC}-\widebat{DC}=\widebat{EC}+\widebat{EB}-\widebat{DC}=\left(\widehat{CB}-\widebat{DC}\right)+\widebat{EB}=\widebat{ED}=2.\widehat{DCE}\)
\(\Rightarrow\widehat{DMC}=\widehat{DCE}\)
Mà \(\widehat{DEC}=\widehat{DCM}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)
\(\Rightarrow\Delta EDC\sim\Delta CDM\left(g-g\right)\Rightarrow\frac{ED}{CD}=\frac{EC}{CM}\Rightarrow CM.ED=CD.EC\) (2)
Từ (1) và (2) ta thấy, muốn chứng minh CM = MA, ta chỉ cần chứng minh EB.DA = CD.EC
Lại có \(\widebat{CE}=\widebat{CB}\Rightarrow CE=CB\)
Vậy ta cần chứng minh: EB.DA = CD.BC
Ta có \(\widehat{DAC}=\frac{\widebat{EC}-\widebat{DC}}{2}=\frac{\widebat{BC}-\widebat{DC}}{2}=\frac{\widebat{DB}}{2}=\widehat{DCB}\)
Vậy nên ta có ngay \(\Delta DBC\sim\Delta DCA\left(g-g\right)\Rightarrow\frac{BD}{CD}=\frac{BC}{CA}\Rightarrow BC.CD=BD.CA\left(3\right)\)
Ta dễ dàng thấy ngay \(\Delta BDA\sim\Delta EBA\left(g-g\right)\Rightarrow\frac{BD}{EB}=\frac{DA}{BA}=\frac{DA}{CA}\Rightarrow EB.DA=BD.CA\left(4\right)\)
Từ (3) và (4) ta có \(EB.DA=BC.CD\)
Từ đó suy ra MC = MA hay M là trung điểm của AC (đpcm).

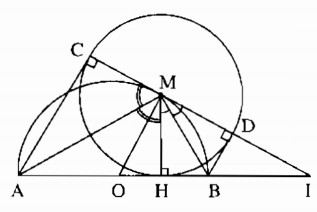
A B M H O C D I
a) Áp dụng tính chất hai tiếp tuyến giao nhau: ^HMC = 2.^AMH; ^HMD = 2.^BMH
Suy ra ^HMC + ^HMB = 2(^AMH + ^BMH) = 1800 => 3 điểm C,M,D thẳng hàng (đpcm).
Có C,M,D thẳng hàng, Do C,D thuộc (M;MH) nên CD là đường kính của (M;MH)
Khi đó MO là đường trung bình của hình thang vuông ACDB => MO // AC // BD
=> MO vuông góc CD => CD là tiếp tuyến của (O) (đpcm).
b) Dễ thấy AC + BD = AH + BH = 2R (R là bán kính của (O)) (không đổi).
c) Áp dụng hệ thức lượng trong tam giác vuông IMO có OH.OI = OM2 = R2 (không đổi).

a, HS tự chứng minh
b, ΔCOD và ΔAMB đồng dạng => MC.MD = O M 2
c, AC = R 3
BD.AC = MC.MD = O M 2
=> BD = R 3 3

Hướng dẫn, ghét hình học phẳng:
Để ý rằng AB vuông góc (M) tại H nên AH, BH cũng là các tiếp tuyến của (M)
- Nối MA, MB
- \(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn (O) nên suy ra...
- AH, AC là 2 tiếp tuyến \(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
Tương tự: \(\widehat{BMD}=\widehat{BMH}\)
\(\Rightarrow\widehat{CMD}=2\left(\widehat{AMH}+\widehat{BMH}\right)\)
b. AC, AH, BD, BH là các tiếp tuyến nên \(\left\{{}\begin{matrix}AC=AH\\BD=BH\end{matrix}\right.\) \(\Rightarrow AC+BD=...\)
c.
AC song song BD (cùng vuông CD), O và M lần lượt là trung điểm AB, CD
\(\Rightarrow OM\) là đtb hình thang vuông ABDC \(\Rightarrow OM\) vuông CD
Hệ thức lượng tam giác vuông OMK: \(OM^2=OH.OK\)
Mà \(OM=\dfrac{AB}{2}\Rightarrow...\)