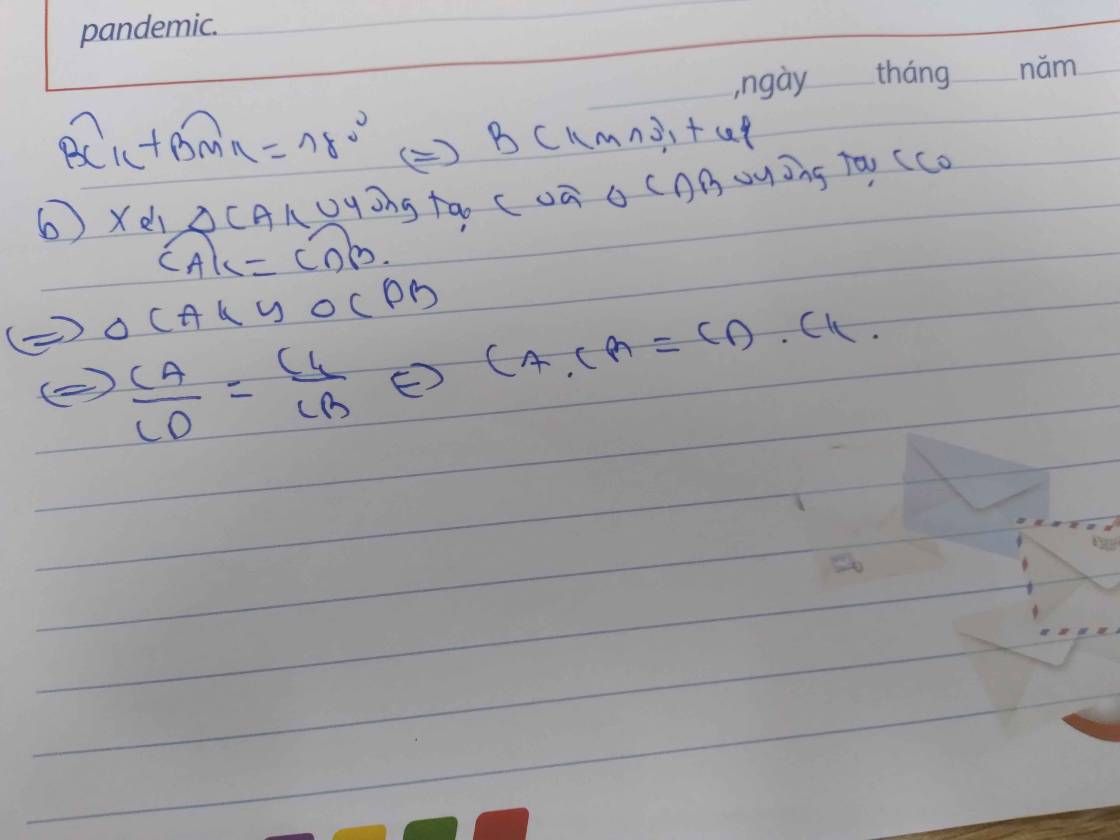Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

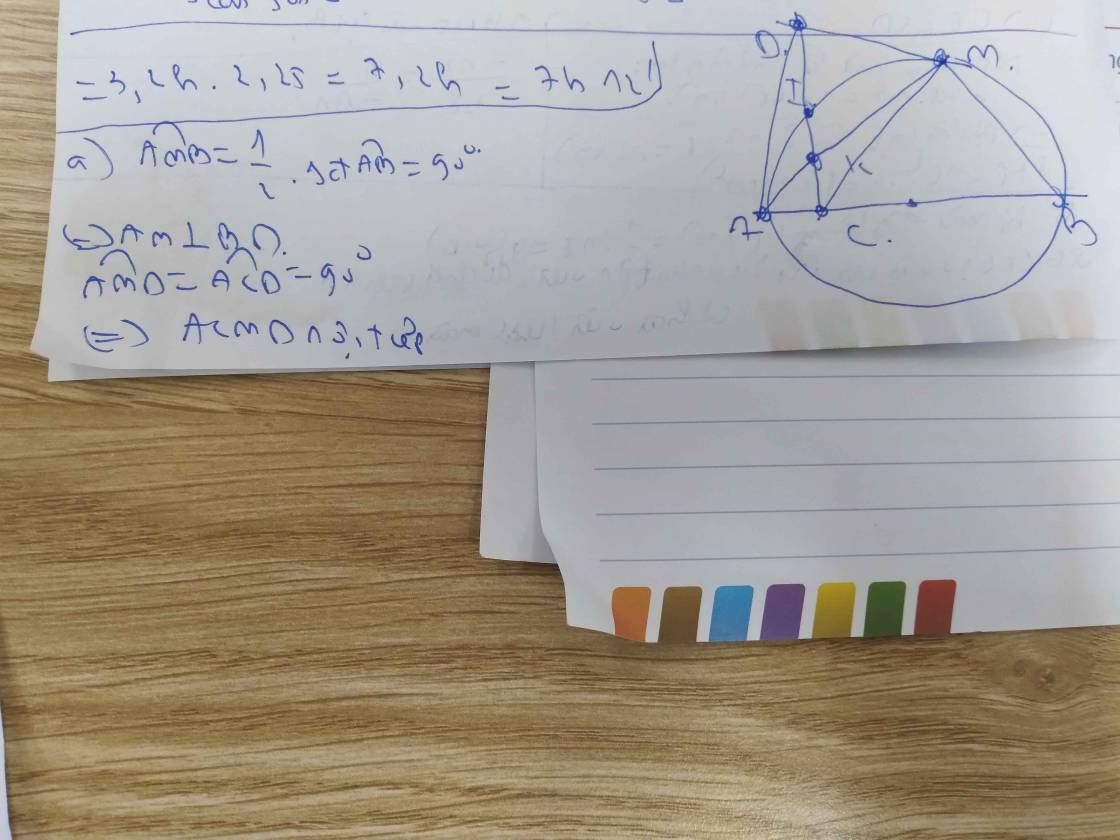
a)MOC vuông tại M => MOC + MCO = 90
mà ICO cân tại I => MCO = COI ; mà COI + COA =90
=> MOC = COA => OC là phân giác AOM
CM tương tự đối với OD ( IOD + DOB =90...)
b) \(\Delta\)AOC =\(\Delta\)MOC (c=g-c)
=> A =90 => CA vuông góc với OA tại A thuộc (O)
=> CA là tiếp tuyến của (O)
- CM tương tự DB là tt
c) theo a
OC là phân giác AOM ; OD là phân giác MOB
mà AOM;MOB là hai góc kề bù => OC vuông góc OD
=>\(\Delta\)COD vuông tại O
\(\Delta\)AMB vuông tại M ( OM =OA=OB =1/2 AB)
mà có góc D = B =COM ( tự cm)
=> \(\Delta\)COD đồng dạng \(\Delta\)AMD ( g-g)
d) \(\Delta\)AOC đồng dạng \(\Delta\)BDO
=>OA/BD = AC/BO => AC.BD = OA.OB = AB/2 .AB/2 = AB2/4

a, xét tứ giác ACMD có:
góc DAC + góc DMC=180 độ( do DAC=90 độ, CMD =90 độ)
vậy ACMD là tứ giác nt
xét tứ giác BCME có:
góc CBE+ góc CME= 180 độ( vì góc CBE= 90 độ, góc CME =90 độ)
vậy tứ giác BCME là tg nt