Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

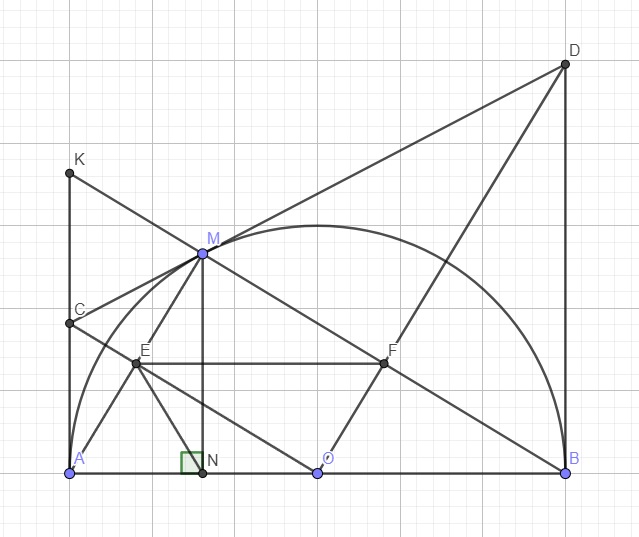
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân

a: Xét tứ giác PAOM có
góc PAO+góc PMO=180 độ
=>PAOM là tứ giác nội tiếp
b: Xét (O) có
PA,PM là tiếp tuyến
nên PA=PM và OP là phân giác của góc MOA(1)
mà OA=OM
nên OP là trung trực của AM
=>OP vuông góc AM
Xét (O) có
QM,QB là tiếp tuyến
nên QM=QB và OQ là phân giác của góc MOB(2)
mà OM=OB
nên OQ là trung trực của MB
=>OQ vuông góc MB tại K
Từ (1), (2) suy ra góc POQ=1/2*180=90 độ
Xét tứ giác MIOK có
góc MIO=góc MKO=góc IOK=90 độ
=>MIOK là hình chữ nhật
Xét ΔOPQ vuông tại O có OM là đường cao
nên MP*MQ=OM^2=R^2
=>AP*QB=OM^2=R^2 ko đổi

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC

* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)