Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
- Vì M,N lần lượt là hình chiếu của A và B trên d (gt) nên ta có
AM và BN cùng vuông góc với d
=> AM song song BN
- Xét tứ giác AMNB có:
AM song song BN(cmt)
=> AMNB là hình thang mà góc AMN = 90* ( AM vuông góc MN)
=> tg AMNB là hình thang vuông.
Vậy...

a: Xét tứ giác ABNM có
AM//BN
góc AMN=90 độ
Do đó: ABNM là hình thang vuông
b: AM//CO
=>gó MAC=góc OCA=góc OAC
=>AC là phân giác của góc BAM

a: Xét tứ giác ABNM có
AM//BN
góc AMN=90 độ
=>ABNM là hình thang vuông
b: AM//CO
=>góc MAC=góc OCA
=>góc MAC=góc OAC
=>AC là phân giác của góc BAM

Ta có: AE // OC
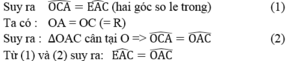
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE

Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90 °
Tam giác ABC vuông tại C có CH ⊥ AB
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
C H 2 = HA.HB (3)
Xét hai tam giác ACH và ACE, ta có:
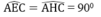
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : ∆ ACH = ∆ ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có:
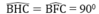
CH = CF (= CE)
BC chung
Suy ra: ∆ BCH = ∆ BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: C H 2 = AE.BF

E 1 A H O B C F d
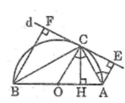
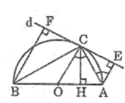
a. Ta có: \(OC\perp d\)(tính chất tiếp tuyến)
\(AE\perp d\) (gt)
\(BF\perp d\) (gt)
Suy ra : OC // AE // BF
Mà OA = OB (= R)
Suy ra: CE = CF ( tính chất đường thẳng song song cách đều )
b. Ta có: AE // OC
\(\Rightarrow\widehat{OCA}=\widehat{EAC}\)( hai góc so le trong ) ( 1 )
Ta có : \(OA=OC\left(=R\right)\)
\(\Rightarrow\Delta OAC\)cân tại O \(\Rightarrow\widehat{OCA}=\widehat{OAC}\)( 2 )
Từ (1)(2) suy ra : \(\widehat{EAC}=\widehat{OAC}\)
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE
c. Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90o
Tam giác ABC vuông tại C có \(CH\perp AB\)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
CH2 = HA . HB (3)
Xét hai tam giác ACH và ACE, ta có :
\(\widehat{AEC}=\widehat{AHC}=90^o\)
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : \(\Delta ACH=\Delta ACE\) (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có :
\(\widehat{AHC}=\widehat{BFC}=90^o\)
CH = CF (= CE)
BC chung
Suy ra: \(\Delta BCH=\Delta BCF\) (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: CH2 = AE . BF
