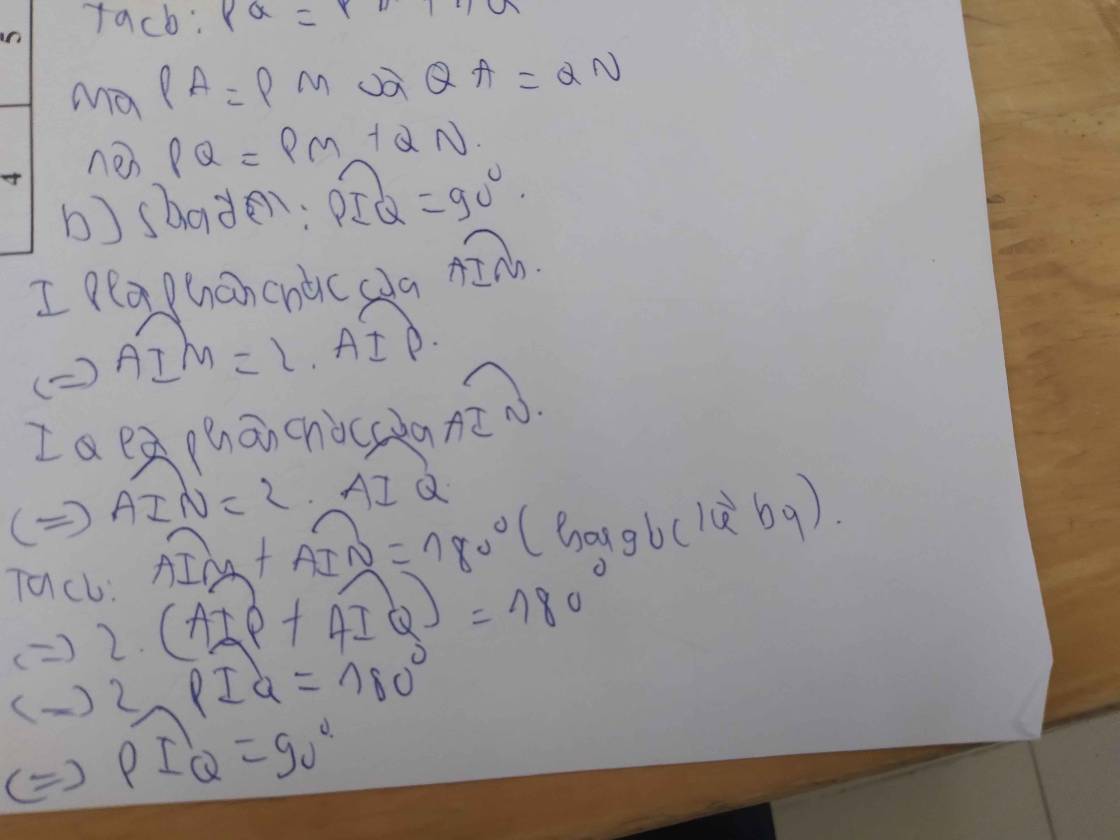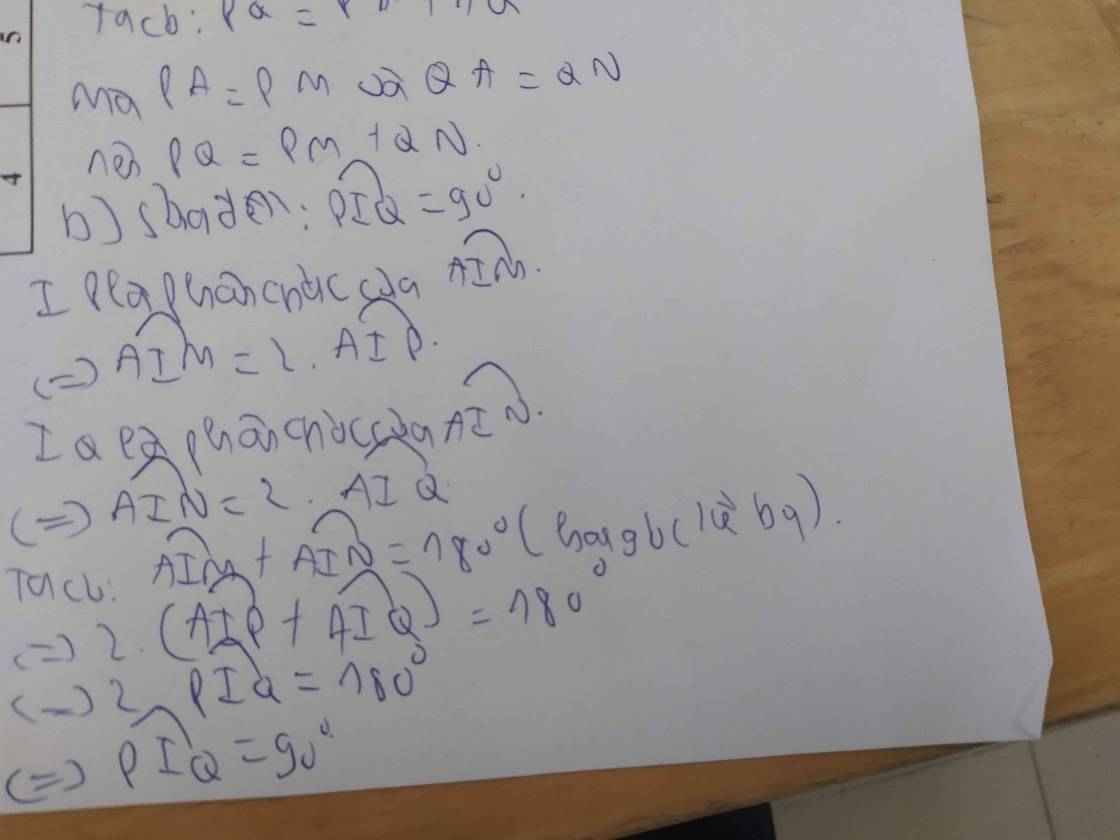Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
PE,PM là tiếp tuyến
=>PE=PM và IP là phân giác của góc EIM(1)
Xét (O) có
QE,QN là tiếp tuyến
=>QE=QN và IQ là phân giác của góc EIN(2)
PQ=PE+EQ
=>PQ=PM+QN
b: Từ (1), (2) suy ra góc PIQ=1/2*180=90 độ
c: Gọi O là trung điểm của PQ
Xét hình thang MNQP có
O,I lần lượt là trung điểm của PQ,MN
=>OI là đường trung bình
=>OI vuông góc MN
=>MN là tiếp tuyến của (O)

a) Để chứng minh CM PQ = PN + NQ, ta sẽ sử dụng định lí Pitago trong tam giác vuông.
Gọi A là giao điểm của tiếp tuyến Mx và Ny. Ta có tam giác AMP và tam giác ANQ là tam giác vuông tại M và N.
Theo định lí Pitago, ta có:
AM^2 = AP^2 + PM^2
AN^2 = AQ^2 + NQ^2
Vì tam giác AMP và tam giác ANQ là tam giác vuông, nên ta có:
AP = AM - PM
AQ = AN - NQ
Thay vào các công thức trên, ta có:
AM^2 = (AM - PM)^2 + PM^2
AN^2 = (AN - NQ)^2 + NQ^2
Mở ngoặc và rút gọn, ta có:
AM^2 = AM^2 - 2AM*PM + PM^2 + PM^2
AN^2 = AN^2 - 2AN*NQ + NQ^2 + NQ^2
Simplifying, we have:
2AM*PM = 2AN*NQ
Chia cả hai vế cho 2, ta có:
AM*PM = AN*NQ
Vì AM = AN (vì là đường kính của nửa đường tròn), nên ta có:
PM = NQ
Do đó, ta có:
PQ = PM + NQ
Vậy, CM PQ = PN + NQ đã được chứng minh.
b) Để chứng minh CM góc PIO = 90 độ, ta sẽ sử dụng tính chất của tiếp tuyến và tiếp tuyến chung.
Gọi O là tâm của nửa đường tròn. Ta có:
Góc PIO = Góc PIM + Góc MIO
Vì PM là tiếp tuyến của đường tròn tại M, nên góc PIM = 90 độ.
Vì Mx và Ny là tiếp tuyến chung, nên góc MIO = góc NIO.
Vậy, góc PIO = 90 độ đã được chứng minh.
c) Để chứng minh CM MN là tiếp tuyến của đường tròn đường kính PQ, ta sẽ sử dụng tính chất của tiếp tuyến và góc chóp đồng quy.
Gọi O là tâm của nửa đường tròn. Ta có:
Góc MON = Góc MOP + Góc NOP
Vì MN là tiếp tuyến của đường tròn tại M, nên góc MOP = 90 độ.
Vì Mx và Ny là tiếp tuyến chung, nên góc NOP = góc NMO.
Vậy, góc MON = 90 độ.
Do đó, MN là tiếp tuyến của đường tròn đường kính PQ đã được chứng minh.

a) Xét (O) có
BI là tiếp tuyến có I là tiếp điểm(gt)
BN là tiếp tuyến có N là tiếp điểm(gt)
Do đó: OB là tia phân giác của \(\widehat{NOI}\)(Tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(\widehat{BOI}=\dfrac{1}{2}\cdot\widehat{NOI}\)
Xét (O) có
AI là tiếp tuyến có I là tiếp điểm(gt)
AM là tiếp tuyến có M là tiếp điểm(gt)
Do đó: OA là tia phân giác của \(\widehat{IOM}\)(Tính chất hai tiếp tuyến cắt nhau)
Suy ra: \(\widehat{AOI}=\dfrac{1}{2}\cdot\widehat{IOM}\)
Ta có: \(\widehat{IOB}+\widehat{IOA}=\widehat{BOA}\)(tia OI nằm giữa hai tia OA và OB)
\(\Leftrightarrow\widehat{AOB}=\dfrac{1}{2}\cdot\left(\widehat{ION}+\widehat{IOM}\right)=\dfrac{1}{2}\cdot180^0\)
hay \(\widehat{AOB}=90^0\)
Vậy: \(\widehat{AOB}=90^0\)

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC