Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

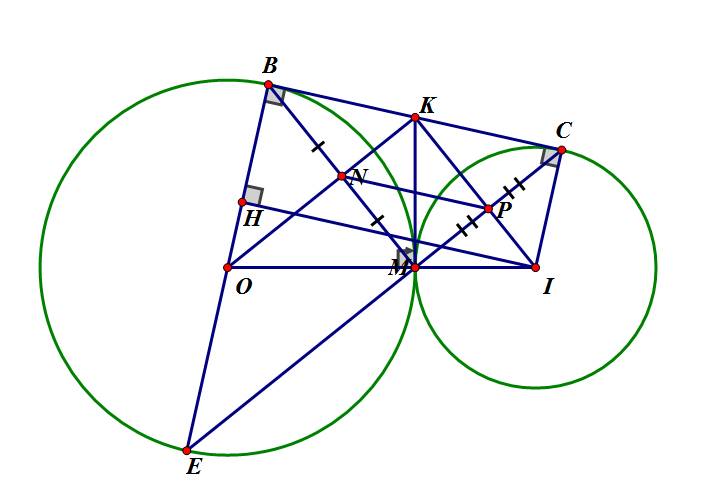
a) Trong (O) có: KB,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KB=KM\left(1\right)\).
Trong (I) có: KC,KM là hai tiếp tuyến cắt nhau tại K.
\(\Rightarrow KC=KM\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow KB=KC\)
△BME nội tiếp đường tròn (O) đường kính BE.
⇒△BME vuông tại MM.
\(\Rightarrow\widehat{BME}=90^0\)
b) Ta có: K thuộc đường trung trực của BM (\(KB=KM\))
O thuộc đường trung trực của BM \(\left(OB=OM\right)\)
⇒OK là đường trung trực của BM mà OK cắt BM tại N.
⇒N là trung điểm BM.
- Ta có: K thuộc đường trung trực của CM (\(KC=KM\))
I thuộc đường trung trực của CM \(\left(IC=IM\right)\)
⇒IK là đường trung trực của CM mà IK cắt CM tại P.
⇒P là trung điểm IK và \(CM\perp IK\) tại P.
Xét △BCM có: N là trung điểm BM, P là trung điểm CM.
⇒NP là đường trung bình của △BCM.
⇒NP//CM.
c) *Hạ \(IH\perp OB\) tại H.
Xét tứ giác BCIH có: \(\widehat{HBC}=\widehat{BCI}=\widehat{BHI}=90^0\)
⇒BCIH là hình chữ nhật.
\(\Rightarrow BC=IH;IC=BH=r\)
Xét △ICK vuông tại C có IP là đường cao:
\(\Rightarrow IK.IP=IC^2=r^2\)
Xét △OHI vuông tại H có:
\(HI^2+OH^2=OI^2\)
\(\Rightarrow HI=\sqrt{OI^2-OH^2}=\sqrt{\left(r+R\right)^2-\left(r-R\right)^2}=\sqrt{4Rr}=2\sqrt{Rr}\)
Mà \(BC=HI\Rightarrow BC=2\sqrt{Rr}\left(1'\right)\)
Ta có: \(2\sqrt{IM.IO-IK.IP}=2\sqrt{r\left(r+R\right)-r^2}=2\sqrt{Rr}\left(2'\right)\)
\(\left(1'\right),\left(2'\right)\Rightarrow BC=2\sqrt{IM.IO-IK.IP}\)

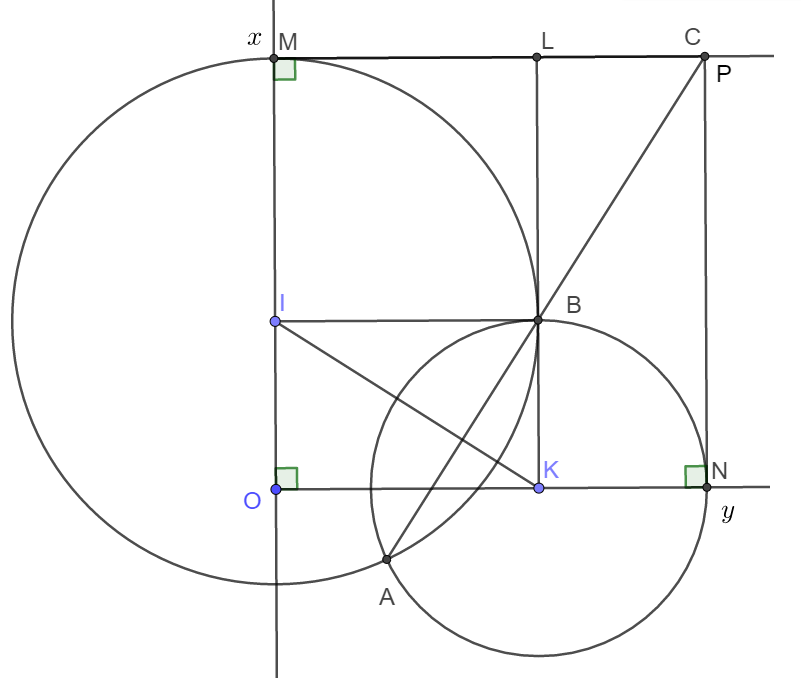
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.



